Прямые, которые не пересекаются, называются параллельными.
Две прямые, перпендикулярные одной и той же прямой, параллельны. На рисунке 1 имеем  и
и  , а значит,
, а значит,  .
.
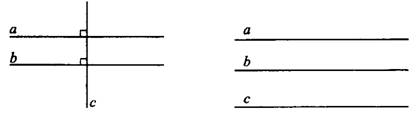
Рис.1 Рис.2
Две прямые, параллельные третьей, также параллельны.
Например, если  и
и  , то
, то  (см. рис. 2).
(см. рис. 2).
Если точка  не лежит на прямой
не лежит на прямой  , то можно провести ровно одну прямую
, то можно провести ровно одну прямую  , проходящую через точку
, проходящую через точку  и параллельную прямой
и параллельную прямой  .
.
Рассмотрим две прямые, пересечённые третьей, которая называется секущей (см. рис. 3).
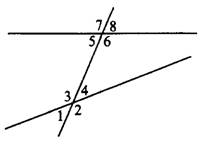
Рис. 3
 и
и  ,
,  и
и  накрест лежащие;
накрест лежащие;  и
и  ,
,  и
и  ,
,  и
и  ,
,  и
и  соответственные;
соответственные;  и
и  ,
,  и
и  - односторонние.
- односторонние.
• Если при пересечении двух прямых третьей образуются равные накрест лежащие углы, то прямые параллельны.
• Если при пересечении двух прямых третьей образуются равные соответственные углы, то прямые параллельны.
• Если при пересечении двух прямых третьей сумма односторонних углов равна 180°, то прямые параллельны.
Верно и обратное. При пересечении параллельных прямых секущей (см. рис. 4) накрест лежащие углы равны ( ,
,  ), соответственные углы равны (
), соответственные углы равны ( ), а сумма односторонних углов равна 180° (
), а сумма односторонних углов равна 180° ( ).
).
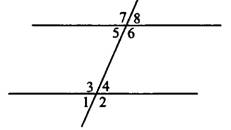
Рис. 4
Расстоянием между двумя параллельными прямыми называется длина перпендикуляра, соединяющего две точки этих прямых.
Задача 1. Докажите, что прямые  и
и  параллельны (см. рис. 5).
параллельны (см. рис. 5).
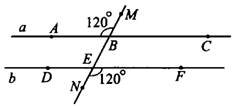
Рис. 5
Решение.
 (как вертикальные углы) и, следовательно,
(как вертикальные углы) и, следовательно,  .
.
Так как соответственные углы  и
и  равны, то прямые
равны, то прямые  и
и  параллельны.
параллельны.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная отрезку и проходящая через его середину. Все точки, лежащие на серединном перпендикуляре к отрезку, равноудалены от его концов (например, на рисунке 6 прямая  — серединный перпендикуляр к отрезку
— серединный перпендикуляр к отрезку  , а значит,
, а значит,  ).
).
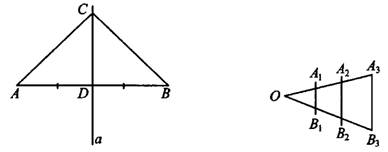
Рис.6 Рис.7
Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Рассмотрим пример (см. рис. 7). Если  и
и  , то
, то  .
.







