В любой треугольник можно вписать окружность, которая будет касаться каждой из его сторон, т. е. иметь с ней одну общую точку. Такая окружность — единственная. Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник (см. рис.1).
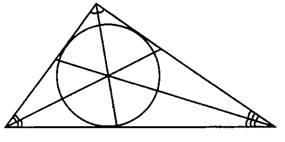
Рис.1
Вокруг любого треугольника можно описать окружность, которая проходит через все его вершины. Такая окружность — единственная. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника (см. рис.2).
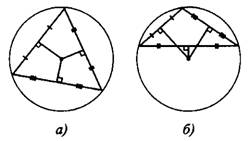
Рис.2
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности ( )
)
Площадь треугольника равна произведению трёх его сторон, делённому на учетверённый радиус описанной окружности  .
.
Если треугольник  вписан в окружность и
вписан в окружность и  , то
, то  — диаметр (см. рис. 3). В этом случае радиус описанной окружности равен половине гипотенузы.
— диаметр (см. рис. 3). В этом случае радиус описанной окружности равен половине гипотенузы.
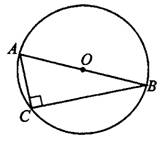
Рис.3
Если в треугольнике один из углов опирается на диаметр описанной окружности, то этот угол — прямой.
Задача 1. На рисунке 4 окружность с центром  описана вокруг
описана вокруг  . Найдите радиус окружности.
. Найдите радиус окружности.
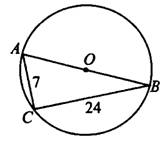
Рис.4
Решение.
 опирается на диаметр. Значит,
опирается на диаметр. Значит,  , по теореме Пифагора
, по теореме Пифагора  ,
,

Ответ: 12,5.
Задача 2. В окружность вписан треугольник. Найдите градусную меру большей из дуг окружности, используя рисунок 5.
Решение.
 вписанный, опирается на дугу
вписанный, опирается на дугу  .
.
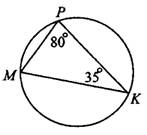
Рис.5
 , поэтому
, поэтому  .
.
Аналогично  .
.  . Большая дуга равна 160°.
. Большая дуга равна 160°.
Ответ: 160.







