Площадь прямоугольника равна произведению его смежных сторон: 
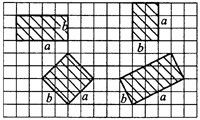
На рисунке 1 приведены чертежи некоторых прямоугольников, у которых показаны смежные стороны  и
и  .
.
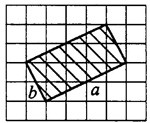
Задача 1. На клетчатой бумаге с клетками размером 1 см х 1 см изображён прямоугольник (см. рис.2). Найдите его площадь в квадратных сантиметрах.
Решение. 1-й способ.
Площадь прямоугольника равна произведению его смежных сторон  и
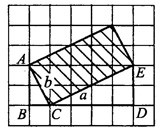
и  . Для того чтобы найти стороны прямоугольника, рассмотрим прямоугольный треугольник
. Для того чтобы найти стороны прямоугольника, рассмотрим прямоугольный треугольник  с катетами
с катетами  = 2 и
= 2 и  = 1 и гипотенузой
= 1 и гипотенузой  = 6 (см. рис. 3).
= 6 (см. рис. 3).
По теореме Пифагора гипотенуза  равна
равна  . Из треугольника
. Из треугольника  с катетами
с катетами  и
и  найдём гипотенузу
найдём гипотенузу  .
.  . Следовательно, площадь прямоугольника
. Следовательно, площадь прямоугольника  .
.
Ответ: 10.
2-й способ.
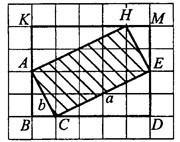
Достроим прямоугольник  до прямоугольника
до прямоугольника  (см. рис.4). Чтобы найти площадь
(см. рис.4). Чтобы найти площадь  , нужно из площади прямоугольника
, нужно из площади прямоугольника  вычесть площади прямоугольных треугольников
вычесть площади прямоугольных треугольников  ,
,  ,
,  и
и  .
.
Так как площадь прямоугольного треугольника равна половине произведения катетов, то площадь каждого из двух больших треугольников ( и
и  ) равна 4, а площадь каждого из двух маленьких треугольников (
) равна 4, а площадь каждого из двух маленьких треугольников ( и
и  ) равна 1. Площадь прямоугольника
) равна 1. Площадь прямоугольника  равна
равна  . Следовательно, площадь искомого прямоугольника будет равна
. Следовательно, площадь искомого прямоугольника будет равна
20 - 1 - 1 - 4 - 4 = 10.
Ответ: 10.
Заметим, что подобным «достраиванием» можно найти площадь любого многоугольника на клетчатой бумаге.
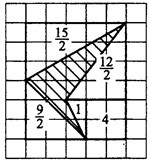
Задача 2. На клетчатой бумаге с клетками размером 1 см х 1 см изображён четырёхугольник (см. рис. 5). Найдите его площадь в квадратных сантиметрах.
Решение.
Достроим четырёхугольник до прямоугольника (см. рис. 5).
Чтобы найти площадь четырёхугольника, нужно из площади прямоугольника со сторонами 5 и 6 вычесть площади четырёх прямоугольных треугольников и квадрата. Попробуйте посчитать площади прямоугольных треугольников самостоятельно, величины этих площадей указаны на рисунке.
Получаем площадь заданного четырёхугольника:
 = 30 - 7,5 - 6 - 1 - 4,5 - 4 = 7 .
= 30 - 7,5 - 6 - 1 - 4,5 - 4 = 7 .
Ответ: 7.







