Иррациональными называются уравнения, в которых переменная содержится под знаком корня (радикала) или под знаком возведения в дробную степень.
Примеры иррациональных уравнений:
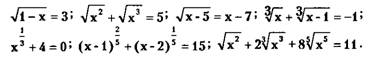
ОСНОВНЫМИ МЕТОДАМИ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ ЯВЛЯЮТСЯ:
1) метод возведения обеих частей уравнения в одну и ту же степень;
2) метод введения новых переменных. Иногда при¬меняют также различные искусственные приемы.
При решении иррациональных уравнений методом возведения обеих частей в четную степень могут появиться посторонние (лишние) корни. Эти корни могут появиться за счет того, что при возведении обеих частей исходного уравнения f(x) = φ(х) в четную степень получается уравнение, являющееся следствием не только уравнения f(x) = φ(x), но и уравнения f(x) = -φ(x), поскольку и (f(x))² =(ф(х))², И (f(x))² =(-ф(х))². Если уравнение f(x) = -φ(х) имеет корни, то именно они являются посторонними корнями исходного уравнения f(x) = φ(x).
Так, например, возьмем уравнение
![]()
Возведя обе части этого уравнения в квадрат, получим
![]()
<=> х² - 15х + 54 = 0. Корнями этого уравнения являются числа x₁ = 9, х₂ = 6. Однако x₁ = 9 является корнем уравнения
![]()
а х₂ = 6 является посторонним корнем (очевидно, что х₂ = 6 является корнем уравнения
![]()
то есть является корнем уравнения f(x) = -ф(х), если исходное уравнение есть f(x) = ф(x)).
Причиной появления посторонних корней, помимо возведения обеих частей уравнения в четную степень, может быть также какая-либо замена (неэквивалентное преобразование), выполняемая, например, в ходе решения уравнения, содержащего кубические радикалы.
Приступая к решению иррационального уравнения, содержащего четные степени радикалов, бывает полезным нахождение множества D допустимых значений переменной (ОДЗ — область допустимых значений), это может облегчить решение исходного уравнения. При этом найденные при решении уравнения значения неизвестных, которые не принадлежат множеству D, являются посторонними. Однако те найденные корни, которые принадлежат D, необходимо проверять, так как и они могут быть посторонними (это будет в том случае, если производились неэквивалентные преобразования в процессе решения уравнения).
Отсюда следует, что в подавляющем большинстве случаев найденные корни иррационального уравнения необходимо проверять. Исключения составляют только случаи, когда на всех этапах решения исходного уравнения производились только эквивалентные (равносильные) преобразования. Однако при этом приходится, как правило, решать неравенства, что иногда отнимает немало времени. Таким образом, нужно либо делать проверку найденных корней, подставляя их значения в исходное уравнение, либо в процессе решения исходного уравнения делать только эквивалентные преобразования, которые не могут привести ни к потере корней, ни к приобретению лишних корней.
Прежде чем приступать к рассмотрению основных методов решения иррациональных уравнений, рассмотрим некоторые несложные иррациональные уравнения, при решении которых основные методы не применяются.
Пример 1. Решить уравнение
![]()
Решение. Поскольку
![]()
где а — любое действительное число, если n — нечетное, m/n>0, то исходное уравнение равносильно такому: х+(х-1)=5 <=> 2х=6 <=> х=3.
Ответ: {3}.
Пример 2. Решить уравнение
![]()
Решение. Находим ОДЗ (область допустимых значений х, или, что то же самое, множество D).
![]()
Таким образом, в данном примере предварительное нахождение ОДЗ оказалось чрезвычайно полезным.
Ответ: ∅.
Пример 3. Решить уравнение
![]()
Решение. Поскольку
![]()
![]()
так как неотрицательное число не может равняться отрицательному.
Ответ: ∅.
Пример 4. Решить уравнение
![]()
Решение. Т. к. для корней четной степени берется всегда арифметическое (неотрицательное) значение корня, то
![]()
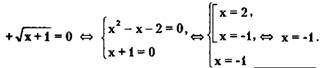
Ответ: {-1}.
Пример 5. Решить уравнение
![]()
Решение. Поскольку х² + 2х + 1 = (х + 1)², х² - 4х + 4 =(х-2)²,
![]()
то исходное уравнение равносильно следующему: |х +1|+|х - 2| = 4.
Решая это уравнение методом интервалов, имеем совокупность трех смешанных систем:
![]()
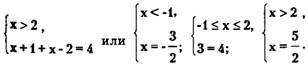
Первая и третья системы имеют решения, а именно, -3/2, 5/2 а вторая — нет.
Ответ: {-3/2, 5/2}






