Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно было бы найти соответствующее значение функции. Имеется четыре основные способа задания функции:
1) аналитический;
2) графический;
3) табличный;
4) словесным описанием.
1) Аналитический способ задания функции. При аналитическом способе задания функция задается с помощью формулы у = f(x), где f(x) — некоторое выражение с переменной х.
Например,
![]()
Замечание 1. В математической литературе чаще всего встречается запись функции с помощью фигурных скобок, если функция задана не одним аналитическим выражением. Такая запись является, по-видимому, не совсем корректной, т. е. вместо фигурных скобок точнее было бы писать прямые скобки. Тем не менее, чтобы не отступать от общепринятых обозначений, мы будем в дальнейшем использовать фигурные скобки.
Если функция задается аналитически, то ее область определения нередко называется естественной областью определения. Это множество всех тех значений х, для каждого из которых формула, определяющая функцию f(x), имеет смысл. Так, например, для функции у = х² естественная область определения — множество всех действительных чисел, Т. е. хє (-∞;+∞)=R. Для функции у естественной областью определения является множество неотрицательных действительных чисел, т. е. хє [0;+∞).
2) При графическом способе задания изображают график функции у = f(x) в системе координат хОу.
Графиком функции называется изображение на координатной плоскости множества упорядоченных пар {(х;у)|у = f(x), х є D(f)}. Каждой упорядоченной паре действительных чисел (х;у) можно поставить в соответствие точку на плоскости. Для этого на плоскости изображают прямоугольную (декартову) систему координат хОу (рис. 1).
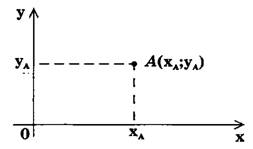
Прямые Ох и Оу взаимно перпендикулярны, О — точка пересечения этих прямых. Ох — ось абсцисс, Оу — ось ординат, 0 — начало координат. На каждой из осей Ох и Оу выбирают положительное направление отсчета (на оси Ох — слева направо, на оси Оу — снизу вверх). Выбирают также единицу измерения
(масштаб). Каждая точка А(хₐ; yₐ) на координатной плоскости имеет две координаты: хₐ — абсциссу, уₐ — ординату. Записывается это так: А(хₐ; yₐ).
Таким образом, график функции y = f(x) есть множество точек координатной плоскости хОу, абсциссы которых есть значения аргумента х, а ординаты — соответствующие значения функции у. Для того чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая, параллельная оси Оу, пересекалась с этим графиком не более чем в одной точке.
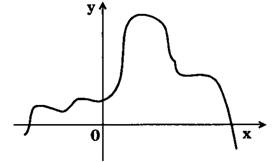
Графический способ удобен тогда, когда задать функцию аналитически довольно трудно (см., например, рис.2)
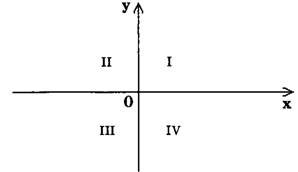
Замечание 2. Оси координат разбивают плоскость на четыре части — I, II, III, IV четверти или координатные углы (рис. 3).
3) Табличный способ задания функции заключается в том что соответствие между элементами множеств D(f) и E(f) задается в форме таблицы.
При этом способе приводится таблица, указывающая значения функции y1, у2,..., уn для имеющихся в таблице значений аргумента x1, х2,..., хn.

Примерами табличного способа задания функции являются, например, таблицы квадратов, квадратных корней, кубов, логарифмов и т. д.
4) При словесном способе задания функции закон, согласно которому значения функции соответствуют значениям аргумента, формулируется словесно. Так, например, размер подоходного налога является функцией заработной платы налогоплательщика.






