Решение задач на бесконечно убывающую геометрическую прогрессию
Пример 1. Обратить периодическую дробь 0,454545...= 0,(45) в обыкновенную.
Решение. Представим исходную дробь в виде суммы:


(так как у нас есть сумма бесконечно убывающей геометрической прогрессии со знаменателем  ).
).
Ответ: 
Пример 2. Сумма бесконечно убывающей геометрической прогрессии 
 , а сумма квадратов всех ее членов
, а сумма квадратов всех ее членов  . Найти четвертый член прогрессии.
. Найти четвертый член прогрессии.
Решение. Прогрессия, у которой каждый член есть квадрат  , то есть
, то есть  , имеет знаменатель
, имеет знаменатель  , который равен квадрату знаменателя заданной прогрессии
, который равен квадрату знаменателя заданной прогрессии  так как
так как

Отсюда имеем систему уравнении

Разделив второе уравнение системы на первое, возведенное в квадрат, получим


Тогда

Ответ:

Пример 3. В равносторонний треугольник со стороной вписан посредством соединения середин его сторон новый треугольник; в этот треугольник тем же способом вписан новый треугольник и так далее до бесконечности. Найти сумму периметров всех этих треугольников и сумму их площадей.
Решение.
Изобразим на рисунке несколько треугольников, удовлетворяющих условию задачи (рис.1).
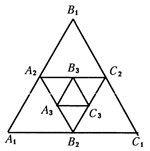
 . Так как
. Так как  — средние линии, то их длины равны
— средние линии, то их длины равны  . Аналогично
. Аналогично  Таким образом, последовательность длин сторон вписанных треугольников образует бесконечно убывающую геометрическую прогрессию
Таким образом, последовательность длин сторон вписанных треугольников образует бесконечно убывающую геометрическую прогрессию  . Последовательность периметров будет получаться путем утроения, т. е.
. Последовательность периметров будет получаться путем утроения, т. е.  . Знаменатель такой прогрессии
. Знаменатель такой прогрессии  а сумма периметров
а сумма периметров  может быть вычислена по формуле для суммы бесконечно убывающей геометрической прогрессии:
может быть вычислена по формуле для суммы бесконечно убывающей геометрической прогрессии:  . Площади полученных правильных треугольников также образуют бесконечно убывающую геометрическую прогрессию
. Площади полученных правильных треугольников также образуют бесконечно убывающую геометрическую прогрессию  . поскольку
. поскольку

и т. д. Знаменатель такой прогрессии
 .
.Отсюда сумма площадей

Ответ:







