Целые рациональные выражения
Целыми рациональными выражениями называются все числовые выражения, а также выражения с переменными, которые могут содержать действия сложения, вычитания, умножения, возведения переменных в натуральную степень. Если рассматривать выражения от одной переменной, то простейшим примером целого рационального выражения является многочлен степени n ∈ N:
![]()
Другие примеры целых рациональных выражений:
![]()
![]()
Выражения
![]()
не являются целыми рациональными, поскольку содержат операции возведения в целую отрицательную степень и деления на переменные.
Дробные рациональные выражения. Основное свойство рациональной дроби
Дробными рациональными выражениями (дробно-рациональными выражениями) называются выражения с переменными, которые могут содержать действия сложения, вычитания, умножения, возведения переменных в натуральную степень и деления на выражения с переменными. Если рассматривать выражения от одной переменной, то примером дробно-рационального выражения является отношение двух многочленов:
![]()
Другие примеры дробных рациональных выражений:
![]()
Рациональной дробью называется выражение
![]()
где Р и Q — рациональные выражения, причем Q обязательно содержит переменные. Примеры рациональных дробей:
![]()
![]()
Основное свойство дроби заключается в том, что числитель и знаменатель дроби можно умножить или разделить на одно и то же отличное от нуля число, одночлен или многочлен,
![]()
если R≠0;
![]()
если R — целое рациональное выражение.
Приведем примеры на использование основного свойства дроби.
Пример 1.
![]()
Пример 2.
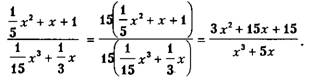
Пример 3.
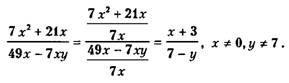
Основное свойство дроби может быть использовано для перемены знаков у членов дроби. Если числитель и знаменатель дроби
![]()
умножить на (-1), то получим
![]()
Отсюда значение дроби не изменится, если одновременно изменить знаки у
числителя и знаменателя. Если же изменить знак только у числителя или только у знаменателя, то и дробь изменит свой знак:
![]()
Также можно записать:
![]()
Пример 4.
![]()
Пример 5.
![]()
Сокращение рациональных дробей
Сократить дробь — это значит разделить числитель и знаменатель дроби на общий множитель. Возможность подобного рода сокращения обусловлена основным свойством дроби.
Для того чтобы сократить рациональную дробь, нужно попытаться разложить на множители числитель и знаменатель. Если числитель и знаменатель имеют общие множители, то дробь можно сократить. Если общих множителей нет, то преобразование дроби посредством сокращения невозможно.
Пример 1. Сократить дробь
![]()
Решение.
![]()
Ответ:
![]()
Пример 2. Сократить дробь
![]()
Решение.
![]()
Ответ:
![]()






