Переменной величиной называется величина, которая принимает различные численные значения.
Постоянная величина — это величина, численные значения которой не меняются. Постоянную величину часто рассматривают как частный случай переменной, у которой все численные значения одинаковы. Постоянную величину нередко называют константой.
Алгебраические выражения — это математические выражения, которые составляются из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в рациональную степень, извлечения корня и с помощью скобок.
Примеры алгебраических выражений:
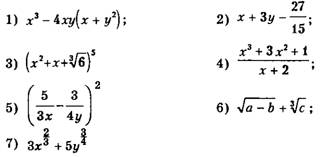
Если алгебраическое выражение не содержит деления на переменные и извлечения корня из переменных, то оно называется целым. Из приведенных выше примеров 1), 2), 3) — целые выражения.
Если алгебраическое выражение составлено из чисел и переменных с помощью действий сложения, вычитания, умножения, возведения в степень с натуральным показателем и деления на выражения с переменными, то оно называется дробным. 4), 5) — примеры дробных алгебраических выражений.
Целые и дробные выражения называются рациональными выражениями. 1), 2), 3), 4), 5) примеры рациональных алгебраических выражений.
Если в алгебраическом выражении используется извлечение корня из переменных (или возведение переменных в дробную степень), то такое алгебраическое выражение называется иррациональным. 6), 7) — примеры иррациональных алгебраических выражений.
Таким образом, алгебраические выражения могут быть рациональными и иррациональными. Рациональные выражения, в свою очередь, бывают целыми и дробными. Рациональные дробные выражения нередко называют дробно-рациональными.
Область определения алгебраического выражения
Множество значений переменных, при которых алгебраическое выражение имеет смысл, называется областью определения алгебраического выражения. Например, областью определения выражения
![]()
является множество всех значений х є R, кроме х = -3, т.е. хе R\{-3}. Область определения выражения
![]()
есть множество пар чисел (a;b), для которых а≠b
Тождественно равные выражения
Два выражения называются тождественно равными, если при всех значениях входящих в них переменных, принадлежащих общей области определения, соответственные значения этих выражений равны.
Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных. Примеры тождеств:
(x+y)² = х² + 2ху + у², x + 0 = x, х •1 = x, (а + b)(a - b) = а² - b².
Верные числовые равенства также называют тождествами,
например:
![]()
— тождества.
Замена одного выражения другим, тождественно равным ему, называется тождественным преобразованием выражения.






