Отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом, называется вектором.
Вектор характеризуется модулем (длиной отрезка) и направлением. Два вектора, имеющие одинаковые модули и направления, равны.
Вектор с началом в точке  и концом в точке
и концом в точке  обозначают
обозначают  или строчной (маленькой) буквой, например
или строчной (маленькой) буквой, например  (см. рис. 1).
(см. рис. 1).
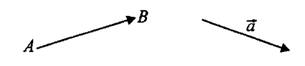
Модуль (длину) вектора обозначают  .
.
Сумма векторов — это вектор, который можно получить двумя способами (см. рис. 2). Заметим, что для любых точек  ,
,  и
и 
 .
.
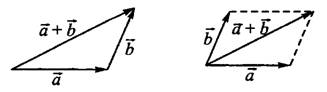
Разность векторов тоже можно получить двумя способами:  или
или  (см. рис. 3).
(см. рис. 3).
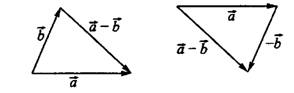
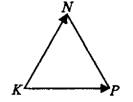
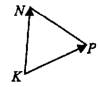
Задача 1. Стороны правильного треугольника  равны 10 (см. рис. 4). Найдите длину вектора
равны 10 (см. рис. 4). Найдите длину вектора  .
.
Решение.

Ответ: 10.
Задача 2. Стороны правильного треугольника  равны 10 (см. рис. 5). Найдите квадрат длины вектора
равны 10 (см. рис. 5). Найдите квадрат длины вектора 
Решение.
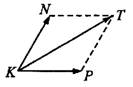
Достроим  до ромба
до ромба  (см. рис. 6).
(см. рис. 6).  Найдём длину
Найдём длину  из
из  с углом
с углом  = 120°. Согласно теореме косинусов,
= 120°. Согласно теореме косинусов, 
Ответ: 300.







