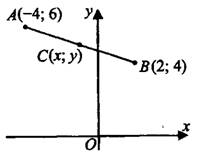
–ó–į–ī–į—á–į 3. –Ě–į–Ļ–ī–ł—ā–Ķ –ĺ—Ä–ī–ł–Ĺ–į—ā—É —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č –ĺ—ā—Ä–Ķ–∑–ļ–į, —Ā–ĺ–Ķ–ī–ł–Ĺ—Ź—é—Č–Ķ–≥–ĺ —ā–ĺ—á–ļ–ł  –ł
–ł  (—Ā–ľ. —Ä–ł—Ā. 6).
(—Ā–ľ. —Ä–ł—Ā. 6).
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–ü—É—Ā—ā—Ć  ‚ÄĒ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į
‚ÄĒ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į  . –Ę–ĺ–≥–ī–į –ĺ—Ä–ī–ł–Ĺ–į—ā–į —ā–ĺ—á–ļ–ł
. –Ę–ĺ–≥–ī–į –ĺ—Ä–ī–ł–Ĺ–į—ā–į —ā–ĺ—á–ļ–ł 
 –ě—Ä–ī–ł–Ĺ–į—ā–į —Ä–į–≤–Ĺ–į 5.
–ě—Ä–ī–ł–Ĺ–į—ā–į —Ä–į–≤–Ĺ–į 5.
–ě—ā–≤–Ķ—ā: 5.
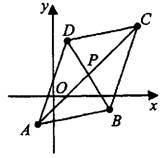
–ó–į–ī–į—á–į 4. –Ę–ĺ—á–ļ–ł  –ł
–ł  —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –≤–Ķ—Ä—ą–ł–Ĺ–į–ľ–ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į. –Ě–į–Ļ–ī–ł—ā–Ķ –į–Ī—Ā—Ü–ł—Ā—Ā—É —ā–ĺ—á–ļ–ł
—Ź–≤–Ľ—Ź—é—ā—Ā—Ź –≤–Ķ—Ä—ą–ł–Ĺ–į–ľ–ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į. –Ě–į–Ļ–ī–ł—ā–Ķ –į–Ī—Ā—Ü–ł—Ā—Ā—É —ā–ĺ—á–ļ–ł  –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ķ–≥–ĺ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–Ķ–Ļ (—Ā–ľ. —Ä–ł—Ā. 7).
–Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ķ–≥–ĺ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–Ķ–Ļ (—Ā–ľ. —Ä–ł—Ā. 7).
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–Ē–ł–į–≥–ĺ–Ĺ–į–Ľ–ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –ł —ā–ĺ—á–ļ–ĺ–Ļ –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –ī–Ķ–Ľ—Ź—ā—Ā—Ź –Ņ–ĺ–Ņ–ĺ–Ľ–į–ľ. –ź–Ī—Ā—Ü–ł—Ā—Ā–į —ā–ĺ—á–ļ–ł  —Ä–į–≤–Ĺ–į
—Ä–į–≤–Ĺ–į

–ě—ā–≤–Ķ—ā: 2,5.
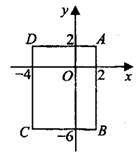
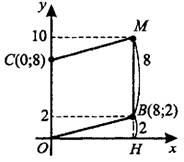
–ó–į–ī–į—á–į 5. –Ě–į–Ļ–ī–ł—ā–Ķ –ĺ—Ä–ī–ł–Ĺ–į—ā—É —Ü–Ķ–Ĺ—ā—Ä–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł (—Ā–ľ. —Ä–ł—Ā. 8), –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ–ĺ–Ľ–ĺ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į  , –≤–Ķ—Ä—ą–ł–Ĺ—č –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ –ł–ľ–Ķ—é—ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ (2;2), (2;‚ÄĒ6), (‚ÄĒ4;‚ÄĒ6), (-4; 2).
, –≤–Ķ—Ä—ą–ł–Ĺ—č –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ –ł–ľ–Ķ—é—ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ (2;2), (2;‚ÄĒ6), (‚ÄĒ4;‚ÄĒ6), (-4; 2).
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–¶–Ķ–Ĺ—ā—Ä –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –Ľ–Ķ–∂–ł—ā –Ĺ–į —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–Ķ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–ł. –Ě–į–Ļ–ī—Ď–ľ –ĺ—Ä–ī–ł–Ĺ–į—ā—É —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ—č  .
.

–ě—ā–≤–Ķ—ā: ‚ÄĒ2.
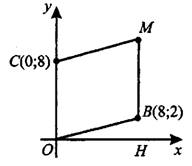
–ó–į–ī–į—á–į 6. –Ę–ĺ—á–ļ–ł  —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –≤–Ķ—Ä—ą–ł–Ĺ–į–ľ–ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į (—Ā–ľ. —Ä–ł—Ā. 9). –Ě–į–Ļ–ī–ł—ā–Ķ –ĺ—Ä–ī–ł–Ĺ–į—ā—É —ā–ĺ—á–ļ–ł
—Ź–≤–Ľ—Ź—é—ā—Ā—Ź –≤–Ķ—Ä—ą–ł–Ĺ–į–ľ–ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į (—Ā–ľ. —Ä–ł—Ā. 9). –Ě–į–Ļ–ī–ł—ā–Ķ –ĺ—Ä–ī–ł–Ĺ–į—ā—É —ā–ĺ—á–ļ–ł  .
.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–ě—Ä–ī–ł–Ĺ–į—ā–į ‚ÄĒ —ć—ā–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į –Ņ–ĺ –ĺ—Ā–ł  . –ě–Ĺ–į —Ä–į–≤–Ĺ–į –ī–Ľ–ł–Ĺ–Ķ –ĺ—ā—Ä–Ķ–∑–ļ–į
. –ě–Ĺ–į —Ä–į–≤–Ĺ–į –ī–Ľ–ł–Ĺ–Ķ –ĺ—ā—Ä–Ķ–∑–ļ–į  (—Ā–ľ. —Ä–ł—Ā. 10).
(—Ā–ľ. —Ä–ł—Ā. 10).
 = 2, —ā–į–ļ –ļ–į–ļ –ĺ—Ä–ī–ł–Ĺ–į—ā–į
= 2, —ā–į–ļ –ļ–į–ļ –ĺ—Ä–ī–ł–Ĺ–į—ā–į  —Ä–į–≤–Ĺ–į 2. –ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ—č–Ķ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į —Ä–į–≤–Ĺ—č, —ā–ĺ
—Ä–į–≤–Ĺ–į 2. –ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ—č–Ķ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į —Ä–į–≤–Ĺ—č, —ā–ĺ  . –Ę–ĺ–≥–ī–į
. –Ę–ĺ–≥–ī–į  .
.
–ě—ā–≤–Ķ—ā: 10.
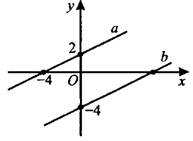
–ó–į–ī–į—á–į 7. –ü—Ä—Ź–ľ–į—Ź –į –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ–ł —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į–ľ–ł (0;2) –ł (-4;0). –ü—Ä—Ź–ľ–į—Ź  –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ—É —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į–ľ–ł (0;‚ÄĒ4) –ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–į –Ņ—Ä—Ź–ľ–ĺ–Ļ
–Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ—É —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į–ľ–ł (0;‚ÄĒ4) –ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–į –Ņ—Ä—Ź–ľ–ĺ–Ļ  (—Ā–ľ. —Ä–ł—Ā. 11). –Ě–į–Ļ–ī–ł—ā–Ķ –į–Ī—Ā—Ü–ł—Ā—Ā—É —ā–ĺ—á–ļ–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ
(—Ā–ľ. —Ä–ł—Ā. 11). –Ě–į–Ļ–ī–ł—ā–Ķ –į–Ī—Ā—Ü–ł—Ā—Ā—É —ā–ĺ—á–ļ–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ  —Ā –ĺ—Ā—Ć—é
—Ā –ĺ—Ā—Ć—é  .
.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
1-–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī.
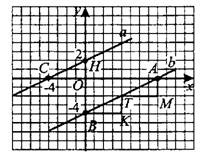
–Ě–į—Ä–ł—Ā—É–Ķ–ľ –ļ–į—Ä—ā–ł–Ĺ–ļ—É –Ĺ–į –ļ–Ľ–Ķ—ā—á–į—ā–ĺ–Ļ –Ī—É–ľ–į–≥–Ķ (—Ā–ľ. —Ä–ł—Ā. 12).
–ź–Ī—Ā—Ü–ł—Ā—Ā–į —ā–ĺ—á–ļ–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ  —Ā –ĺ—Ā—Ć—é
—Ā –ĺ—Ā—Ć—é  —Ä–į–≤–Ĺ–į –ī–Ľ–ł–Ĺ–Ķ –ĺ—ā—Ä–Ķ–∑–ļ–į
—Ä–į–≤–Ĺ–į –ī–Ľ–ł–Ĺ–Ķ –ĺ—ā—Ä–Ķ–∑–ļ–į  . –Ę–į–ļ –ļ–į–ļ –Ņ—Ä—Ź–ľ—č–Ķ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č, —É–≥–Ľ—č
. –Ę–į–ļ –ļ–į–ļ –Ņ—Ä—Ź–ľ—č–Ķ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č, —É–≥–Ľ—č  –ł
–ł  —Ä–į–≤–Ĺ—č, –ī–ĺ—Ā—ā—Ä–ĺ–ł–ľ 2 —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į
—Ä–į–≤–Ĺ—č, –ī–ĺ—Ā—ā—Ä–ĺ–ł–ľ 2 —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į  –ł
–ł  , —Ä–į–≤–Ĺ—č—Ö —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ—É
, —Ä–į–≤–Ĺ—č—Ö —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ—É  .
.
 .
.
–ě—ā–≤–Ķ—ā: 8.
2-–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī.
–Ę—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł  –ł
–ł  –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č –Ņ–ĺ —ā—Ä—Ď–ľ —É–≥–Ľ–į–ľ (—Ā–ľ. —Ä–ł—Ā. 13), –∑–Ĺ–į—á–ł—ā, –ł—Ö —Ā—ā–ĺ—Ä–ĺ–Ĺ—č –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č.
–Ņ–ĺ–ī–ĺ–Ī–Ĺ—č –Ņ–ĺ —ā—Ä—Ď–ľ —É–≥–Ľ–į–ľ (—Ā–ľ. —Ä–ł—Ā. 13), –∑–Ĺ–į—á–ł—ā, –ł—Ö —Ā—ā–ĺ—Ä–ĺ–Ĺ—č –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č.  , —ā–ĺ–≥–ī–į
, —ā–ĺ–≥–ī–į  .
.
–ě—ā–≤–Ķ—ā: 8.
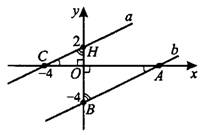
–ó–į–ī–į—á–į 8. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–Ľ–ĺ–≤–ĺ–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā –Ņ—Ä—Ź–ľ–ĺ–Ļ, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ–ł —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į–ľ–ł (12; 0) –ł (0; 12) (—Ā–ľ. —Ä–ł—Ā. 14).
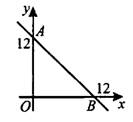
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–£–≥–Ľ–ĺ–≤–ĺ–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā –Ņ—Ä—Ź–ľ–ĺ–Ļ —Ä–į–≤–Ķ–Ĺ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā—É —É–≥–Ľ–į, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ņ—Ä—Ź–ľ–į—Ź –ĺ–Ī—Ä–į–∑—É–Ķ—ā —Ā –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–Ķ–ľ –ĺ—Ā–ł
 (—ā–į–ľ, –≥–ī–Ķ –Ĺ–į –ĺ—Ā–ł —Ā—ā—Ä–Ķ–Ľ–ĺ—á–ļ–į). –í –Ĺ–į—ą–Ķ–Ļ –∑–į–ī–į—á–Ķ —ć—ā–ĺ —É–≥–ĺ–Ľ
(—ā–į–ľ, –≥–ī–Ķ –Ĺ–į –ĺ—Ā–ł —Ā—ā—Ä–Ķ–Ľ–ĺ—á–ļ–į). –í –Ĺ–į—ą–Ķ–Ļ –∑–į–ī–į—á–Ķ —ć—ā–ĺ —É–≥–ĺ–Ľ  (—Ā–ľ. —Ä–ł—Ā. 15).
(—Ā–ľ. —Ä–ł—Ā. 15).
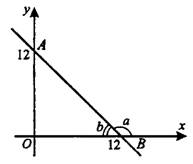
–ě–Ĺ —ā—É–Ņ–ĺ–Ļ, –∑–Ĺ–į—á–ł—ā, –Ķ–≥–ĺ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ļ –ł –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é —Ä–į–≤–Ķ–Ĺ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā—É —É–≥–Ľ–į  . –†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ļ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ
. –†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ļ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ  —Ā –ļ–į—ā–Ķ—ā–į–ľ–ł
—Ā –ļ–į—ā–Ķ—ā–į–ľ–ł  = 12 –ł
= 12 –ł  = 12. –Ę–į–Ĺ–≥–Ķ–Ĺ—Ā —É–≥–Ľ–į
= 12. –Ę–į–Ĺ–≥–Ķ–Ĺ—Ā —É–≥–Ľ–į  —Ä–į–≤–Ķ–Ĺ
—Ä–į–≤–Ķ–Ĺ  . –Ę–į–Ĺ–≥–Ķ–Ĺ—Ā —É–≥–Ľ–į
. –Ę–į–Ĺ–≥–Ķ–Ĺ—Ā —É–≥–Ľ–į  —Ä–į–≤–Ķ–Ĺ ‚ÄĒ1. –£–≥–Ľ–ĺ–≤–ĺ–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā –Ņ—Ä—Ź–ľ–ĺ–Ļ —Ä–į–≤–Ķ–Ĺ ‚ÄĒ1.
—Ä–į–≤–Ķ–Ĺ ‚ÄĒ1. –£–≥–Ľ–ĺ–≤–ĺ–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā –Ņ—Ä—Ź–ľ–ĺ–Ļ —Ä–į–≤–Ķ–Ĺ ‚ÄĒ1.
–ě—ā–≤–Ķ—ā: ‚ÄĒ1.







