Трапеция. Готовимся к ОГЭ по математике. Модуль 2. Урок 51

Трапецией называется четырёхугольник, у которого две стороны параллельны (основания трапеции), а две другие не параллельны. Пример трапеции — на рисунке 1, где $BC$ и $AD$ — основания, а $AB$ и $CD$ — боковые стороны.
Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон ($MK$ в трапеции $ABCD$ на рисунке 1).

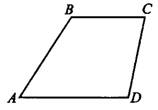
Рис.1

Средняя линия параллельна основаниям и равна их полусумме: $\displaystyle MK=\frac{1}{2}\left ( BC+AD \right )$.
Площадь трапеции равна полусумме оснований, умноженной на высоту: $\displaystyle S=\frac{BC+AD}{2}\cdot BH$ (см. рис.2).

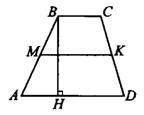
Рис.2

Трапеция называется равнобедренной, если её боковые стороны равны ($AB=CD$ в трапеции $ABCD$ на рисунке 3).

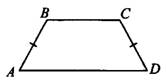
Рис.3

В равнобедренной трапеции углы при каждом из оснований равны: ($\displaystyle \angle A=\angle D,\angle B=\angle C$ на рисунке 3). Верно и обратное утверждение: если в трапеции углы при основании равны, то трапеция равнобедренная.
В равнобедренной трапеции диагонали равны. Верно и обратное утверждение: если в трапеции диагонали равны, то она равнобедренная.
Задача 1. Найдите площадь трапеции на рисунке 4.

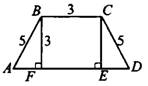
Рис.4

Решение.
Заметим, что $BEFC$ — параллелограмм (так как стороны попарно параллельны), откуда $FE=BC$.
Из $\displaystyle \bigtriangleup ABF$ по теореме Пифагора найдём $\displaystyle AF=\sqrt{AB^{2}-BF^{2}}=\sqrt{25-9}=\sqrt{16}=4$. Аналогично $\displaystyle ED=4$. $\displaystyle AD=AF+FE+ED=4+3+4=11$.
$\displaystyle S_{ABCD}=\frac{1}{2}\left ( BC+AD \right )\cdot BF=\frac{42}{2}=21$.
Ответ: 21.