Прямоугольник — это параллелограмм, у которого все углы прямые (см. рис.1).

Рис.1
Признак прямоугольника: если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Рассмотрим рисунок 2. Если мы знаем, что  — параллелограмм и
— параллелограмм и  , то мы можем утверждать, что
, то мы можем утверждать, что  — прямоугольник.
— прямоугольник.
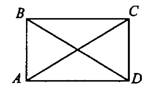
Рис.2
Площадь прямоугольника равна произведению его смежных сторон:  (на рисунке 2).
(на рисунке 2).
Диагонали любого прямоугольника равны.
Другим видом параллелограмма является ромб — четырёхугольник, все стороны которого равны между собой (см. рис.3).
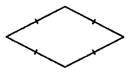
Рис.3
Ромб является параллелограммом, диагонали которого взаимно перпендикулярны ( на рисунке 4).
на рисунке 4).
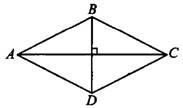
Рис.4
Признак ромба: если в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом. Если  — параллелограмм и
— параллелограмм и  , то
, то  — ромб (см. рис.4).
— ромб (см. рис.4).
Площадь ромба равна половине произведения его диагоналей.  для ромба ABCD на рисунке 4.
для ромба ABCD на рисунке 4.
Квадрат — это такой прямоугольник, у которого все стороны равны (см. рис. 5).
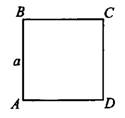
Рис.5
Квадрат также является ромбом, а потому сочетает в себе свойства и прямоугольника, и ромба.
Диагональ квадрата  , если
, если  — сторона квадрата.
— сторона квадрата.
Площадь квадрата равна квадрату его стороны, то есть  (см. рис.5).
(см. рис.5).
Если известна диагональ квадрата  , его площадь можно найти по формуле
, его площадь можно найти по формуле  .
.
Задача 1. Найдите площадь и высоту ромба  , изображённого на рисунке 6.
, изображённого на рисунке 6.
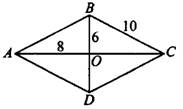
Рис.6
Решение.
 , так как ромб — параллелограмм и диагонали точкой пересечения делятся пополам.
, так как ромб — параллелограмм и диагонали точкой пересечения делятся пополам.
 .
.
С другой стороны,  , где
, где  — высота ромба.
— высота ромба. 
Ответ: 96; 9,6.
Задача 2. Укажите номера верных утверждений.
1) В равностороннем треугольнике все углы равны 90°.
2) Любой прямоугольник является ромбом.
3) В равнобедренной трапеции углы при основании равны.
4) Диагонали параллелограмма точкой пересечения делятся пополам.
5) Сумма двух соседних углов ромба может быть больше 180°.
Решение.
Утверждение 1) неверно, так как в равностороннем треугольнике все углы равны 60°.
Утверждение 2) неверно, так как легко привести пример прямоугольника, который не является ромбом (см. рис.7).
Утверждение 3) верно, оно является свойством равнобедренной трапеции.
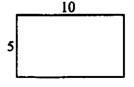
Рис.7
Утверждение 4) верно, оно является свойством параллелограмма.
Утверждение 5) неверно, так как сумма соседних углов любого параллелограмма равна 180°.
Ответ: 34.







