Движение плоскости — это отображение плоскости на себя, сохраняющее расстояние.
Осевая симметрия
Осевая симметрия задаётся прямой, которую называют осью симметрии. Две точки  и
и  называются симметричными относительно прямой
называются симметричными относительно прямой  , если эта прямая проходит через середину отрезка
, если эта прямая проходит через середину отрезка  и перпендикулярна к нему (см. рис. 1).
и перпендикулярна к нему (см. рис. 1).
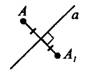
Рис.1
Если точка лежит на прямой  , то она симметрична сама себе относительно этой прямой.
, то она симметрична сама себе относительно этой прямой.
У фигуры есть ось симметрии — прямая  , если для каждой точки фигуры симметричная ей относительно прямой а точка также принадлежит этой фигуре. На рисунке 2 изображены оси симметрии некоторых фигур. Если мысленно «перегнуть» фигуру по оси симметрии, то части фигуры должны совпасть.
, если для каждой точки фигуры симметричная ей относительно прямой а точка также принадлежит этой фигуре. На рисунке 2 изображены оси симметрии некоторых фигур. Если мысленно «перегнуть» фигуру по оси симметрии, то части фигуры должны совпасть.
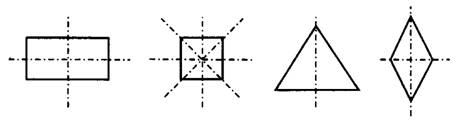
Рис.2
Центральная симметрия
Центральная симметрия задаётся точкой. Эта точка называется центром симметрии.
Две точки  и
и  называются симметричными относительно точки
называются симметричными относительно точки  , если
, если  — середина отрезка
— середина отрезка  (см. рис. 3).
(см. рис. 3).
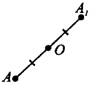
Рис.3
Фигура называется симметричной относительно точки  , если для каждой точки фигуры симметричная ей относительно
, если для каждой точки фигуры симметричная ей относительно  точка также принадлежит этой фигуре. На рисунке 4 изображены центры симметрии некоторых фигур.
точка также принадлежит этой фигуре. На рисунке 4 изображены центры симметрии некоторых фигур.
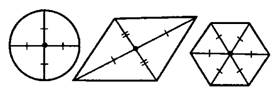
Рис.4
Параллельный перенос
Параллельный перенос задаётся вектором. При параллельном переносе на вектор  точка
точка  отображается в точку
отображается в точку  , если
, если  .
.
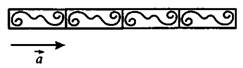
Рис.5
Рисунок 5 получен применённым трижды параллельным переносом фигуры
![]()
на вектор  , равный длине этой фигуры.
, равный длине этой фигуры.
Поворот
Поворот задаётся неподвижной точкой и углом поворота.
Поворотом плоскости вокруг точки  на угол а называют отображение плоскости на себя, при котором точка
на угол а называют отображение плоскости на себя, при котором точка  отображается в точку
отображается в точку  так, что
так, что  и
и  (см. рис. 6).
(см. рис. 6).
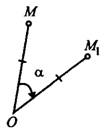
Рис.6
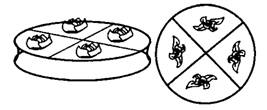
Рис.7
На рисунке 7 торт порезан на куски, каждый из которых получился из соседнего поворотом на 90°. При повороте на 90° торт «переходит сам в себя».
Задача 1. а) Колесо имеет 12 спиц (см. рис. 8). Сколько осей симметрии имеет колесо?
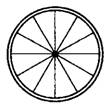
Рис.8
б) Сколько всего осей симметрии имеет фрагмент, изображённый на рисунке?
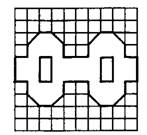
Рис.9
в) Сколько всего осей симметрии имеет фигура, изображённая на рисунке 10?
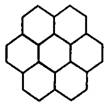
Рис.10
Решение.
а) Оси симметрии проходят как «по спицам», так и посередине между спицами (как показано на рисунке 11). Всего 12 осей симметрии.
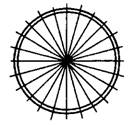
Рис.11
Ответ: 12.
б) Оси симметрии проходят так, как показано на рисунке 12. Таких осей 2.
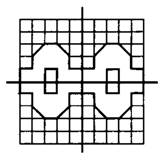
Рис.12
Ответ: 2.
в) Оси симметрии проходят так, как показано на рисунке 13. Таких осей 6.
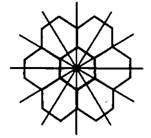
Рис.13
Ответ: 6.
Задача 2. Пол на кухне разбит на маленькие равные квадраты, некоторые из них чёрного цвета (см. рис. 14). Какое минимальное количество квадратов чёрного цвета нужно ещё приклеить на пол, чтобы полученная фигура стала симметричной относительно диагонали кухни — прямой  ?
?
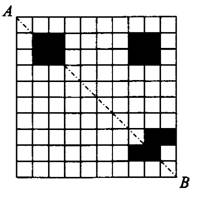
Рис.14
Решение.
На рисунке 15 выделены пунктиром квадраты, которые нужно приклеить на пол, чтобы полученная фигура стала симметричной относительно диагонали  . Видим, что таких квадратов 5.
. Видим, что таких квадратов 5.
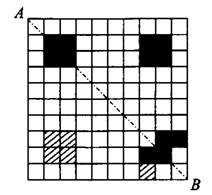
Рис.15
Ответ: 5.
Задача 3. Карточку, изображённую на рисунке 16, повернули на 90° по часовой стрелке.
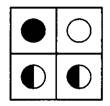
Рис.16
Какая из карточек, изображённых на рисунке 17, при этом получилась?
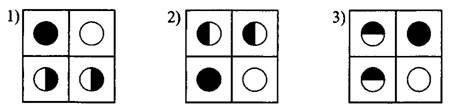
Рис.17
Решение.
При повороте карточки на 90° по часовой стрелке можно получить только карточку 3 на рисунке 17, потому что, например, чёрный кружок повернётся и попадёт в правый верхний угол (см. рис. 18). Убедитесь, что и другие круги перейдут на места кружков карточки 3 рисунка 17.
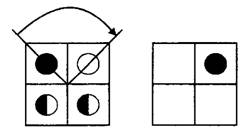
Рис.18
Ответ: 3.
Задача 4. Воздушный шар взлетел из пункта  и летит с постоянной скоростью 10 км/ч в течение 3 часов. Затем он поворачивает на 90° и летит с той же скоростью ещё 4 часа и прибывает в пункт
и летит с постоянной скоростью 10 км/ч в течение 3 часов. Затем он поворачивает на 90° и летит с той же скоростью ещё 4 часа и прибывает в пункт  . Найдите расстояние от
. Найдите расстояние от  до
до  в километрах.
в километрах.
Решение.
Нарисуем схему полёта шара (см. рис. 19). Видим, что до точки поворота шар пролетел расстояние  км, а после точки поворота — расстояние
км, а после точки поворота — расстояние  км. По теореме Пифагора найдём
км. По теореме Пифагора найдём  .
.  (км).
(км).
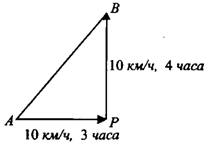
Рис.19
Ответ: 50.