Как правило, в задачах практической геометрии используется подобие треугольников. Напомним некоторые определения и теоремы.
Часто встречаются фигуры, которые имеют разные размеры, но одинаковую форму, например, все круги или все квадраты. Такие фигуры называют подобными.
Треугольники  и
и  подобны друг другу (
подобны друг другу ( ), если
), если  и
и  , где
, где  называют коэффициентом подобия (см. рис. 1).
называют коэффициентом подобия (см. рис. 1).
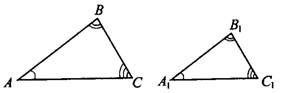
Рис.1
В подобных треугольниках медианы, биссектрисы и высоты пропорциональны с тем же коэффициентом.
Признаки подобия треугольников
1. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Например, если  то
то  (см. рис. 2).
(см. рис. 2).
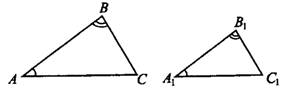
Рис.2
2. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими двумя сторонами, равны, то такие треугольники подобны.
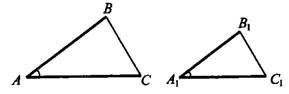
Рис.3
Например, если  и
и  , то
, то  (см. рис. 3).
(см. рис. 3).
3. Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого, то такие треугольники подобны.
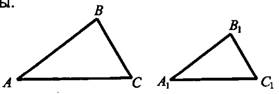
Рис.4
Например, если  , то
, то  (см. рис. 4).
(см. рис. 4).
Теорема Пифагора.
Квадрат гипотенузы равен сумме квадратов катетов.
Например,  (см. рис. 5).
(см. рис. 5).
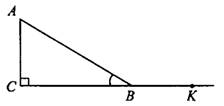
Рис.5
Задача 1. От столба к палатке «Мороженое» натянут провод длиной 13 м, который закреплён на стене палатки на высоте 3 м от земли (см. рис. 6). Вычислите высоту столба, если расстояние от палатки до столба равно 12 м.
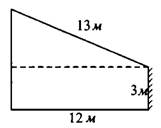
Рис.6
Решение.
В  (см. рис. 7)
(см. рис. 7)  м,
м,  м. По теореме Пифагора имеем
м. По теореме Пифагора имеем  . Отсюда
. Отсюда  м.
м.
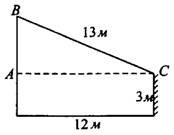
Рис.7
Учитывая, что высота палатки 3 м, найдём высоту столба: 5м + 3м = 8м.
Ответ: 8.
Задача 2. Определите ширину реки  (см. рис. 8), если
(см. рис. 8), если  м,
м,  м,
м,  м,
м,  (Ответ дайте в метрах.)
(Ответ дайте в метрах.)
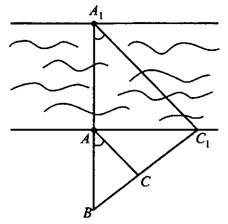
Рис.8
Решение.
На местности отметим точки  и
и  так, чтобы они находились на одной прямой с точкой
так, чтобы они находились на одной прямой с точкой  . На берегу отметим точки
. На берегу отметим точки  и
и  так, чтобы
так, чтобы  была параллельна
была параллельна  .
.
Получим  ,
,
 (м).
(м).
 (м).
(м).
Ответ: 42.
Задача 3. Проектор полностью освещает экран  высотой 60 см, расположенный на расстоянии 300 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран
высотой 60 см, расположенный на расстоянии 300 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран  высотой 150 см, чтобы он был полностью освещен, если настройки проектора остаются неизменными (см. рис. 9)?
высотой 150 см, чтобы он был полностью освещен, если настройки проектора остаются неизменными (см. рис. 9)?
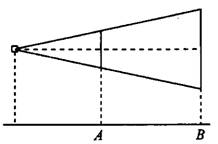
Рис.9
Решение.
Из рисунка 10  , значит
, значит  (см).
(см).
Здесь используется свойство, что высоты подобных треугольников ( и
и  ) относятся так же, как и стороны (
) относятся так же, как и стороны ( )
)
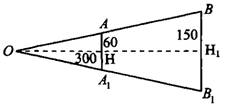
Рис.10
Ответ: 750.
Задача 4. Человек ростом 1,8 м стоит на расстоянии 20 шагов от фонарного столба и отбрасывает тень длиной в 20 шагов. Опре¬делите высоту столба в метрах.
Решение.
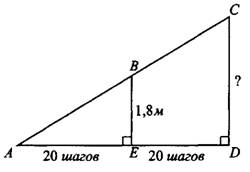
Рис.11
Рассмотрим рисунок 11.

 (м)
(м)
Ответ: 3,6.







