Площадь круга равна произведению числа  на квадрат радиуса:
на квадрат радиуса:

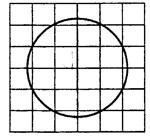
Задача 1. Найдите площадь  круга, считая стороны клеток равными 1 (см. рис. 1). В ответе укажите
круга, считая стороны клеток равными 1 (см. рис. 1). В ответе укажите  .
.
Решение.
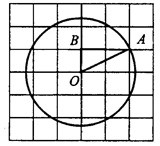
Площадь круга равна произведению числа  на квадрат радиуса. Найдём радиус. Из центра
на квадрат радиуса. Найдём радиус. Из центра  проведём радиус
проведём радиус  . В треугольнике
. В треугольнике  сторона
сторона  — гипотенуза, катеты равны 1 и 2 (см. рис. 2).
— гипотенуза, катеты равны 1 и 2 (см. рис. 2).
Найдём гипотенузу по теореме Пифагора. 
Площадь круга 
Ответ: 5.
Задача 2. На клетчатой бумаге нарисовано два круга (см. рис. 3). Площадь внутреннего круга равна 3. Найдите площадь заштрихованной фигуры.
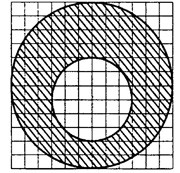
Решение.
Радиус  внутреннего круга — 3 клетки, его площадь равна
внутреннего круга — 3 клетки, его площадь равна  . Радиус внешнего круга — 6 клеток, то есть
. Радиус внешнего круга — 6 клеток, то есть  , поэтому его площадь равна
, поэтому его площадь равна  Площадь заштрихованной фигуры равна разности 12 — 3 = 9.
Площадь заштрихованной фигуры равна разности 12 — 3 = 9.
Ответ: 9.
Площадь сектора с углом  градусов равна
градусов равна 
Задача 3. Найдите площадь  сектора с углом 18 градусов и радиусом 4. В ответе укажите
сектора с углом 18 градусов и радиусом 4. В ответе укажите  .
.
Решение.
Посчитаем площадь сектора по формуле 
Ответ: 0,8.
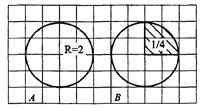
Задача 4. Найдите площадь  заштрихованного сектора, считая стороны клеток равными 1 (см. рис. 4). В ответе укажите
заштрихованного сектора, считая стороны клеток равными 1 (см. рис. 4). В ответе укажите  .
.
Решение.
На рисунке 4A) площадь круга с радиусом  = 2 равна
= 2 равна 
На рисунке 4В) площадь сектора составляет  от площади круга (если круг разделить на 4 равные части, то одна из них как раз и будет равна заданному сектору), то есть
от площади круга (если круг разделить на 4 равные части, то одна из них как раз и будет равна заданному сектору), то есть

Можно было решать задачу по-другому. Площадь сектора равна площади круга, делённой на 4.

Ответ: 1.
Задача 5. Найдите площадь  заштрихованных секторов на рисунках C и D, считая стороны клеток равными 1 (см. рис. 5).
заштрихованных секторов на рисунках C и D, считая стороны клеток равными 1 (см. рис. 5).
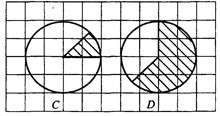
В ответе укажите  .
.
Решение. Посчитаем, какая часть круга закрашена. Проведя дополнительные линии (см. рис. 6), видим, что сектор на рисунке 6C) составляет - часть круга, а сектор на рисунке 6D) составляет
 частей круга (круг разделён на 8 равных частей, и закрашено 5 таких частей).
частей круга (круг разделён на 8 равных частей, и закрашено 5 таких частей).
Находим площади секторов на рисунках 6C) и 6D).
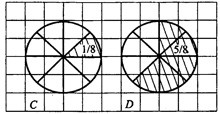
1-й способ.
Поделим площадь круга на 8, получим площадь сектора на рисунке 6C), потом умножим эту площадь на 5, получим площадь сектора на рисунке 6D).

Ответ: 0,5 и 2,5.
2-й способ. Найдём площадь  круга.
круга.

Ответ: 0,5 и 2,5.







