Высоты в прямоугольном треугольнике. Готовимся к ЕГЭ по математике. Геометрия. Урок 21

В прямоугольном треугольнике две высоты совпадают с катетами. Третья высота, проведённая из вершины прямого угла, делит треугольник на два прямоугольных треугольника, углы которых равны соответственно углам исходного треугольника.
Задача 1. В треугольнике $ABC$ угол $C$ равен 90°, высота $\displaystyle CH=2\sqrt{54},\; BC=15.$ Найдите $\displaystyle \cos B.$
Решение.

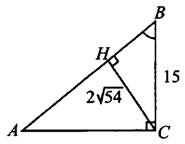
Косинусом угла называют отношение прилежащего катета к гипотенузе. Рассмотрим прямоугольный треугольник $CHB$ с прямым углом $H$ и катетами $BH$ и $HC$ (см. рис. 1). Найдём в нём катет $BH$. $\displaystyle BH^{2}=BC^{2}-HC^{2},\; BH^{2}=15^{2}-(2\sqrt{54})^{2}=225-216=9,$
$\displaystyle BH=\sqrt{9}=3.\; \cos B=\frac{BH}{BC}=\frac{3}{15}=0,2.$
Ответ: 0,2.
Задача 2. Найдите тангенс угла $CAB$, изображённого на рисунке 2. В ответе укажите значение тангенса, умноженное на 3.

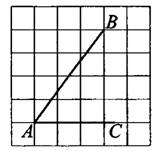
Решение.
Достроим угол до прямоугольного треугольника $ABC$ (см. рис. 3).

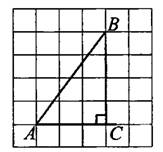
Тангенсом угла называют отношение противолежащего катета к прилежащему.
$\displaystyle tg BAC=\frac{BC}{AC}=\frac{4}{3}$. Значение тангенса, умноженное на 3, равно 4.
Ответ: 4.