Функция вида у = k/x (k≠0) называется обратной пропорциональностью; k называется коэффициентом обратной пропорциональности. Областью определения функции является множество D(f) = (-∞;0) и (0;+∞) = R\{0}.
Графиком функции у = k/x является гипербола.
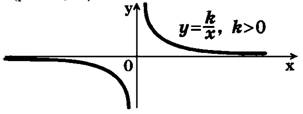
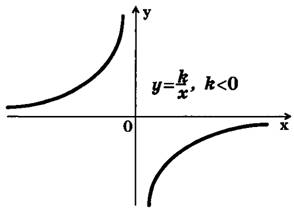
Если k>0, то ветви гиперболы расположены в I и III координатных угла если k<0, то ветви гиперболы расположены в II и IV координатных углах (рис. 1, 2).
Рассмотрим более подробно функцию у = k/x при k = 1 (у = 1/х).
Функция у = 1/x
Составляем таблицу, учитывая, что при х = 0 функция не определена (табл. 1).
Таблица 1

Строим график функции у = 1/x. Это гипербола (рис. 3).
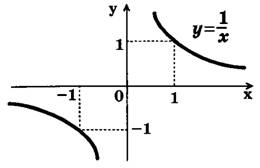
Свойства функции у = 1/x:
а) D(f) = (-∞;0) и (0;+∞) = R\{0};
б) E(f) = (-∞;0) и (0;+∞) =R\{0};
в) функция у = 1/х не имеет нулей, так как уравнение 1/х = 0 не имеет корней, график функции у = 1/х не пересекает ось Ох;
г) функция принимает отрицательные значения при хє(-∞;0) и положительные значения при хє(0;+∞);
д) функция у=1/х убывает при хє(-∞;0), а также при хє(0;+оо);
е) функция не имеет экстремумов;
ж) f(—х) = —f(x) => функция у = 1/х нечетная, ее график симметричен относительно начала координат;
з) график функции у = 1/хне пересекает ось Оу, но при неограниченном приближении х к нулю ветви гиперболы неограниченно приближаются к оси Оу. При неограниченном увеличении х ветви гиперболы неограниченно приближаются к оси Ох, нигде ее не пересекая. Говорят, что оси Ох и Оу асимптоты гиперболы у = 1/х, ось Оу — вертикальная асимптота графика функции у = 1/х, ось Ох — горизонтальная асимптота графика функции у = 1/х.






