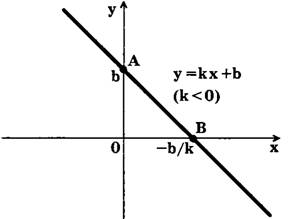
Функция, заданная формулой у = kx+b, где к и b — некоторые фиксированные числа, называется линейной.
Областью определения линейной функции у = kx+b является множество всех действительных чисел R = (-∞,∞).
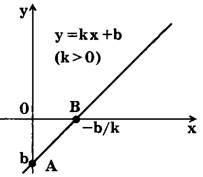
График линейной функции у = kx+b есть прямая линия. Для построения графика у = kx+b достаточно знать координаты двух точек этого графика. Взяв х=0 => у=b => А(0; b) — точка пересечения графика с осью Оу. Взяв у=0 => х=-b/k (k≠0) => B(-b/k;0) — точка пересечения графика с осью Ох. Таким образом, точки пересечения графика функции у = kx+b с осями координат будут B(-b/k;0), А(0; b), если к≠0 (рис. 1, 2).
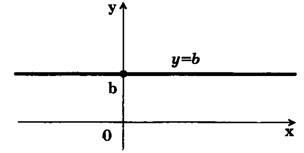
При k = 0 получаем прямую у = b, которая параллельна оси Ох и совпадает с осью Ох, если b = 0 (рис. 3).
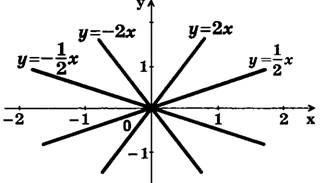
Функция вида у = kх (k≠0) называется прямой пропорциональностью, где k — коэффициент прямой пропорциональности. График функции у = kх есть прямая, которая проходит через начало координат. На рис. 4 изображены графики функций у = kх при k = +1/2, k = -1/2, k = -2, k = +2.
Рассмотрим функции у = х и у = —х, получающиеся из у = kx+b, когда b = 0, к = ±1.
Функция у= х
Составим таблицу, взяв несколько значений х и соответствующих значений у (табл.1).
Таблица 1
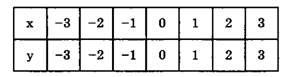
Замечание. Для линейной функции у = kx+b достаточно задать координаты двух точек.
Графиком функции у = х является прямая линия, которая проходит через начало координат. Ее называют биссектрисой 1-го и 3-го координатных углов (рис. 5).
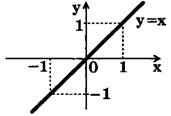
Свойства функции у = х:
а) D(f) = R;
б) E(f) = R;
в) нули функции: у = 0 при х = 0 (функция у = х имеет только один нуль в начале координат);
г) функция принимает отрицательные значения при х є (-∞;0); функция принимает положительные значения при х є (0;+∞);
д) функция возрастает на всей области определения;
е) функция не имеет экстремумов;
ж) у(-х) = -у(х) => функция у = х нечетная, ее график симметричен относительно начала координат.
Функция у = -х
Составим таблицу (табл. 2).
Таблица 2
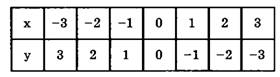
Графиком функции у = -х является прямая линия, которая проходит через начало координат. Ее называют биссектрисой 2-го и 4-го координатных углов (рис. 6).
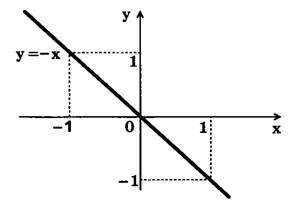
Свойства функции у = -х:
а) D(f) = R;
б) E(f) = R;
в) нули функции: у = 0 при х = 0 (функция у = х имеет только один нуль в начале координат);
г) функция принимает отрицательные значения при х є (0;+∞), Функция принимает положительные значения при х є (-∞;0);
д) функция убывает на всей области определения;
е) функция не имеет экстремумов;
ж) у(-х) = -у(х) => функция у = х нечетная, ее график сиvметричен относительно начала координат.