Геометрическая интерпретация неравенств

Геометрическая интерпретация неравенств
Решение неравенств можно показать геометрически на числовой оси. Так, если мы имеем строгое неравенство $x>a$, то геометрически это множество изображается в виде той части числовой прямой, которая лежит справа от точки с абсциссой $x=a$. При этом правее точки $x=a$ наносят штриховку (рис. 1), а саму точку $x=a$ обычно изображают в виде светлого кружка (говорят, что точку $x=a$ «выкалывают»).

Если имеем нестрогое неравенство $x\leq b$, то на числовой оси наносят штриховку слева от точки $x= b$ (рис. 2), при этом точку $x= b$ обычно закрашивают в черный цвет, т.е. изображают темной точкой.

При решении систем линейных неравенств, состоящих из двух неравенств, можно изображать решения с помощью двух числовых осей или с помощью одной оси, с помощью дуг или без дуг, без помощи штриховок или с помощью штриховок , нанося штриховки, имеющие разный угол наклона относительно числовой прямой, снизу и сверху или только сверху (снизу).
Пример 1. Решить систему неравенств, используя геометрическую интерпретацию

$$\left\{\begin{matrix} 2x-1<3,\\ 3x+2\geq -7. \end{matrix}\right.$$

Решение.

$$\left\{\begin{matrix} 2x-1<3,\\ 3x+2\geq -7, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x<1+3,\\ 3x\geq -2-7, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x<4,\\ 3x\geq -9, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x<2,\\ x\geq -3. \end{matrix}\right.$$

Дадим четыре варианта геометрической интерпретации примера 1.
1 вариант (с использованием двух числовых осей).
На одной числовой прямой отмечаем все те значения х, при которых выполняется первое неравенство системы, а на второй числовой прямой, расположенной под первой,— все те значения х, при которых выполняется второе неравенство системы (рис. 3). Сравнение этих двух результатов показывает, что оба неравенства одновременно будут выполниться при всех значениях х, заключенных от (-3) до (+2), т.е. $-3\leq x<2\Leftrightarrow x\in [-3;2).$

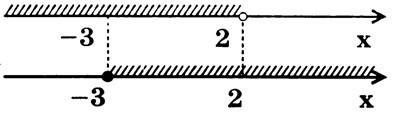
2 вариант (с использованием одной числовой оси и штриховок снизу и сверху оси). На числовую ось наносим штриховки, расположенные выше и ниже числовой прямой, и находим пересечение решений неравенств, образующих исходную систему.

$$\left\{\begin{matrix} 2x-1<3,\\ 3x+2\geq -7, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x<2,\\ x\geq -3. \end{matrix}\right.$$

С помощью координатной прямой (рис. 4) находим, что множество решений исходной системы есть полуинтервал [-3;2).

3 вариант (с использованием одной оси, дуг и штриховок).

$$\left\{\begin{matrix} 2x-1<3,\\ 3x+2\geq -7, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x<2,\\ x\geq -3. \end{matrix}\right.$$

На числовую ось наносим заданные множества $x<2$ и $x\geq -3$ при помощи дуг и штриховок с разным углом наклона к координатной прямой (рис. 5). Искомое множество изображено двойной штриховкой, при помощи наложения двух штриховок.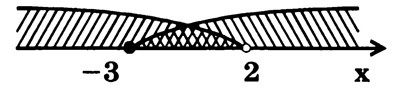

4 вариант (с использованием одной оси и дуг)

$$\left\{\begin{matrix} 2x-1<3,\\ 3x+2\geq -7, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x<2,\\ x\geq -3. \end{matrix}\right.$$

На числовую ось наносим заданные множества $x<2$ и $x\geq -3$ при помощи только одних дуг, а штриховку наносим только там, где заданные множества пересекаются (рис. 6).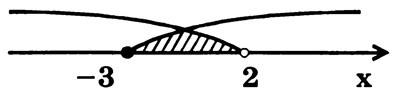

Ответ: $x\in[-3;2).$
Пример 2. Решить систему неравенств

$$\left\{\begin{matrix} 4x+3<7,\\ 2x+1>5. \end{matrix}\right.$$

Решение.

$$\left\{\begin{matrix} 4x+3<7,\\ 2x+1>5, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4x<7-3,\\ 2x>5-1, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4x<4,\\ 2x>4, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x<1,\\ x>2. \end{matrix}\right.$$

Таким образом, любое число, удовлетворяющее обоим неравенствам одновременно, должно быть меньше 1 и больше 2 (рис. 7). Но таких чисел не существует. Поэтому данная система неравенств не выполняется ни при каких значениях $x$, т. е. $x \in$Ø. О таких системах говорят, что они несовместны (геометрически это означает, что нет наложения штриховок).

Ответ: $x\in$Ø.
Пример 3. Решить систему неравенств

$$\left\{\begin{matrix} 2x+1\geq 7,\\ 3x-1\leq 8. \end{matrix}\right.$$

Решение.

$$\left\{\begin{matrix} 2x+1\geq 7,\\ 3x-1\leq 8, \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 3,\\ x\leq 3. \end{matrix}\right.$$

Изображая данные множества с помощью дуг и штриховок (рис.8), видим, что оба неравенства будут одновременно выполняться только при $x=3$.

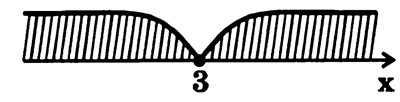
Ответ: {3}.
Пример 4. Решить совокупность неравенств

$$\left [ \begin{matrix} 4x+3<7,\\ 2x+1>5. \end{matrix} \right.$$

Решение.

$$\left [ \begin{matrix} 4x+3<7,\\ 2x+1>5, \end{matrix} \right. \Leftrightarrow \left [ \begin{matrix} x<1,\\ x>2. \end{matrix} \right.$$

С помощью числовой прямой (рис.9) находим, что решением заданной совокупности является множество, состоящее из двух полубесконечных интервалов, т. е.

$$\left [ \begin{matrix} x<1,\\ x>2, \end{matrix} \right. \Leftrightarrow x\in(-\propto ;1)\bigcup (2;\propto)$$

Oтвет:

$$x\in(-\propto ;1)\bigcup (2;\propto)$$

.
Пример 5. Решить совокупность неравенств

$$\left [ \begin{matrix} 2x+1<7,\\ 3x-1<-1. \end{matrix} \right.$$

Решение.

$$\left [ \begin{matrix} 2x+1<7,\\ 3x-1<-1. \end{matrix} \right. \Leftrightarrow \left [ \begin{matrix} x<3,\\ x<0. \end{matrix} \right.$$

С помощью координатной прямой (рис. 10) находим, что решением исходной совокупности неравенств есть полубесконечный интервал $(-\propto ;3)$.

Ответ: $x \in (-\propto ;3).$
Пример 6. Решить совокупность неравенств

$$\left [ \begin{matrix} 2x-1<3,\\ 3x+2\geq -7. \end{matrix} \right.$$

Решение.

$$\left [ \begin{matrix} 2x-1<3,\\ 3x+2\geq -7. \end{matrix} \right. \Leftrightarrow \left [ \begin{matrix} x<2,\\ x\geq -3. \end{matrix} \right.$$

С помощью числовой прямой (рис. 11) находим, что решением заданной совокупности неравенств является вся числовая прямая, т. е.

$$x\in(-\propto ;\propto ).$$

Ответ: $x\in(-\propto ;\propto ).$