Метод замены переменной при решении рациональных неравенств
Многие неравенства удобно решать, применяя метод замены переменной (метод подстановки).
Пример 1. Решить неравенство  . Решение. Сделав замену переменной
. Решение. Сделав замену переменной  , получаем
, получаем  . Корни уравнения
. Корни уравнения  есть
есть  .
Отсюда
.
Отсюда  Поскольку
Поскольку  , то получаем
, то получаем
 2,\; (a)\\ x^{2}-x<6 \; (b) \end{matrix}\right." />
2,\; (a)\\ x^{2}-x<6 \; (b) \end{matrix}\right." />
 2 \Leftrightarrow x^{2}-x-2>0 \Leftrightarrow (x+1)(x-2)>0 \Leftrightarrow \left[ \begin{matrix} x<-1,\\ x>2. \end{matrix} \right." />
2 \Leftrightarrow x^{2}-x-2>0 \Leftrightarrow (x+1)(x-2)>0 \Leftrightarrow \left[ \begin{matrix} x<-1,\\ x>2. \end{matrix} \right." />Решаем неравенство (b):

 2,\\ x^{2}-x<6 \end{matrix} \right. \Leftrightarrow \left\{\begin{matrix} \left[ \begin{matrix} x<-1,\\ x>2, \end{matrix} \right.\\ -2
2,\\ x^{2}-x<6 \end{matrix} \right. \Leftrightarrow \left\{\begin{matrix} \left[ \begin{matrix} x<-1,\\ x>2, \end{matrix} \right.\\ -2
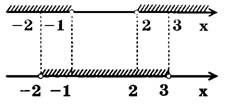
Ответ: 
Пример 2. Решить неравенство  Решение.
Решение.
Обозначив  , получаем из исходного неравенства
, получаем из исходного неравенства  Отсюда исходное неравенство равносильно следующему неравенству:
Отсюда исходное неравенство равносильно следующему неравенству:
 0,\\ x^{2}+6x+14<9 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x\in R,\\ x^{2}+6x+5<0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x\in R,\\ -5
0,\\ x^{2}+6x+14<9 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x\in R,\\ x^{2}+6x+5<0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x\in R,\\ -5
 0" /> для любого
0" /> для любого  , поскольку дискриминант квадратного трехчлена
, поскольку дискриминант квадратного трехчлена 
Ответ:







