Решение иррациональных неравенств

Рассмотрим более сложные иррациональные неравенства.
Иррациональное неравенство $\sqrt{f(x)}<g(x)$ равносильно системе неравенств, т. е.$\sqrt{f(x)}<g(x)\Leftrightarrow \left\{\begin{matrix} f(x)\geq 0,\\ g(x)>0,\\ \left ( \sqrt{f(x)} \right )^{2}<\left ( g(x) \right )^{2} \end{matrix}\right.$ Иррациональное неравенство $\sqrt{f(x)}>g(x)$ равносильно совокупности двух систем неравенств,
т. е. $\sqrt{f(x)}>g(x)\Leftrightarrow \left [ \begin{matrix} \left\{\begin{matrix} f(x)\geq 0,\\ g(x)\geq 0,\\ \left ( \sqrt{f(x)} \right )^{2}>\left ( g(x) \right )^{2}; \end{matrix}\right.\\ \left\{\begin{matrix} f(x)\geq 0,\\ g(x)<0. \end{matrix}\right. \end{matrix} \right.$
Замечание. Если рассмотреть неравенства $\sqrt{f(x)}\leq g(x)$ и $\sqrt{f(x)}\geq g(x)$, то эти неравенства эквивалентны приведенной выше системе неравенств и совокупности двух систем неравенств, в которых знаки строгих неравенств везде заменены на знаки нестрогих, кроме неравенства $g(x)<0$, которое остается неизменным. Пример 1. Решить неравенство $\sqrt{x+31}<x+1$.
Решение.
$\sqrt{x+31}<x+1\Leftrightarrow \left\{\begin{matrix} x+31\geq 0,\\ x+1>0,\\ \left ( \sqrt{x+31} \right )^{2}<\left ( x+1 \right )^{2} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq -31,\;\; (a)\\ x>-1,\; \; (b)\\ x+31<x^{2}+2x+1.(c) \end{matrix}\right.$ Неравенство (c) равносильно следующему:

$$x^{2}+x-30>0\Leftrightarrow (x+6)(x-5)>0\Leftrightarrow \left [ \begin{matrix} x<-6,\\ x>5. \end{matrix} \right.$$

Множества, полученные при решении неравенств (а), (b), (c), необходимо пересечь. Для этого, во избежание ошибок, лучше всего начертить три оси и нанести на каждую из осей полученные множества решений.
Полученные множества пересекаются при $x>5$ (рис.1).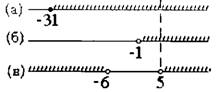

Ответ: $x\in (5;\infty )$.
Пример 2. Решить неравенство $\sqrt{5x-4}<x$. Решение.

$$\sqrt{5x-4}<x\Leftrightarrow \left\{\begin{matrix} 5x-4\geq 0,\\ x>0,\\ \left ( \sqrt{5x-4} \right )^{2}<x^{2} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{4}{5},\\ x>0,\\ 5x-4\leq x^{2} \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{4}{5},\; (a)\\ x>0,\; (b)\\ \left [ \begin{matrix} x<1,\\ x>4. \end{matrix} \right.(c) \end{matrix}\right.$$

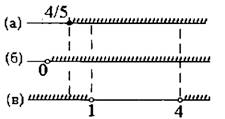
Пересекая множества, полученные при решении неравенств (а), (b), (c) (рис.2), получаем решение исходного неравенства: $x\in \left [ \frac{4}{5};1 \right )\bigcup \left ( 4;+\infty \right )$.
Ответ: $x\in \left [ \frac{4}{5};1 \right )\bigcup \left ( 4;+\infty \right )$.
Пример 3. Решить неравенство $\sqrt{x+2}>x+\frac{1}{2}$.
Решение.

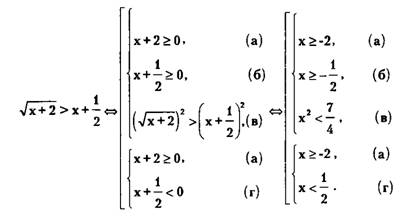
Решая неравенство (в), получаем

$$x^{2}<\frac{7}{4} \Leftrightarrow x^{2}<\left ( \frac{\sqrt{7}}{2} \right )^{2}\Leftrightarrow x^{2}-\left ( \frac{\sqrt{7}}{2} \right )^{2}<0\Leftrightarrow \left ( x-\frac{\sqrt{7}}{2} \right )\left ( x+\frac{\sqrt{7}}{2} \right )<0\Leftrightarrow -\frac{\sqrt{7}}{2}<x<\frac{\sqrt{7}}{2}.$$

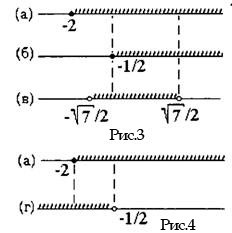
Пересекая множества, полученные при решении неравенств (а), (б), (в) (рис.3), получаем $-\frac{1}{2}\leq x <\frac{\sqrt{7}}{2}.$ Пересекая множества, полученные при решении неравенств (а) и (г) (рис.4), получаем $-2\leq x <-\frac{1}{2}.$ Решение исходного неравенства есть объединение множеств:

$$\left [ -2;-\frac{1}{2} \right )\bigcup \left [ -\frac{1}{2};\frac{\sqrt{7}}{2} \right )=\left [ -2;\frac{\sqrt{7}}{2} \right ).$$

Ответ: $x\in \left [ -2;\frac{\sqrt{7}}{2} \right ).$
Пример 4. Решить неравенство $\sqrt{x^{2}-4x}>x-3.$
Решение.
$\sqrt{x^{2}-4x}>x-3\Leftrightarrow$

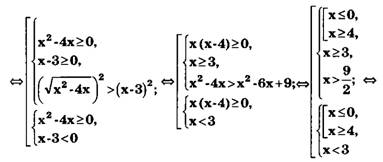
$$\Leftrightarrow \left [ \begin{matrix} x>\frac{9}{2},\\ x\leq 0 \end{matrix} \right. \Leftrightarrow x\in \left (-\infty ;0 \right ]\bigcup \left ( \frac{9}{2};\infty \right ).$$

Ответ: $x\in \left (-\infty ;0 \right ]\bigcup \left ( \frac{9}{2};\infty \right ).$