Выражение f(x,y) называется симметрическим, если при замене х на у, у на х оно не изменяется.
Примеры симметрических выражений
f(x,y)=x+y; f(x,y) = х² +у²; f(x,y) = x³+y³;
![]()
Выражения (х+у) и ху называются основными симметрическими многочленами с двумя переменными. Все симметрические выражения с двумя переменными выражаются через основные симметрические многочлены, например:
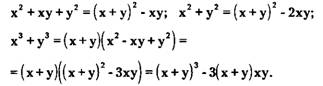
Симметрической системой уравнений называется система, все уравнения которой симметрические. Решать симметрическую систему можно, например, с помощью замены переменных, где новыми переменными являются основные симметрические многочлены.
Пример 1. Решить систему
![]()
Решение.
Поскольку х²+у² =(х + у)²-2ху, то, положив x + y = U, ху = V, приходим к следующей системе:
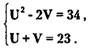
Из этой системы находим
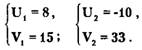
Отсюда исходная система эквивалентна следующей совокупности систем:
![]()
Первая система совокупности имеет решения (3;5),(5;3); вторая система решений не имеет.
Ответ: {(3;5);(5;3)}.
Пример 2. Решить систему
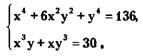
Решение.
х⁴ + 6х²у² + у⁴ = (х² + у²)² + 4х²у² - ((х + у)² - 2ху)² + 4(ху)²,
х³у + ху³ = ху( x² + у²) = ху(( х + у)² - 2ху).
Положим х + у = U, ху = V, тогда заданная система сводится к следующей:
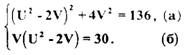
Из уравнения (б) последней системы
![]()
подставляя в (а), получаем
![]()
<=> 4V⁴ - 136V² + 900 = 0 <=> V⁴ - 34V² + 225 = 0.
Решая это биквадратное уравнение, находим V = ±5, V = ±3.
Из (б)
![]()
Подставляя найденные значения V, получаем:
V = 5 => U²=16 <=> U = ±4; V = 3 => U² =16<=>U = ±4
(для V=—5, V=—3 действительных значений U не существует).
Отсюда относительно U, V система имеет решения
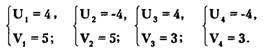
Таким образом, исходная система равносильна совокупности систем:
![]()
Первая и вторая системы решений не имеют, третья система имеет решения (1;3);(3;1), четвертая система имеет решения (—1;—3), (-3;-1).
Ответ: {(1;3);(3;1);(-1;-3);(-3;-1)}.
Симметрические системы уравнений






