Говорят, что число а больше числа b, и пишут а>b, если разность а-b — положительное число. Если разность а-b отрицательное число, то говорят, что число а меньше числа b и пишут а<Ь. Согласно этим определениям любое положительное число больше нуля, любое отрицательное число меньше нуля и меньше любого положительного числа. Для любых заданных чисел а и b верно одно и только одно из соотношений: a>b, a<b, a=b. С геометрической точки зрения неравенство а<b (а>b) означает, что точка а расположена на координатной прямой левее (правее) точки b.
Знаки "<" и ">" называют знаками строгих неравенств. Используют также знаки ![]() — знаки нестрогих неравенств.
— знаки нестрогих неравенств.
Запись
![]()
означает, что верно одно из двух: или число а меньше числа b, или число а равно числу b. Например,
![]()
— верные числовые неравенства,
![]()
— неверное числовое неравенство.
Неравенства а<b и с>d (a>b, c<d) называют неравенствами противоположного смысла (или противоположных знаков). Если числа а, b, с таковы, что а<b и b<с, то вместо этих двух неравенств используется запись а<b<с. Такое неравенство называется двойным.
Пример. Сравнить числа 4/5 и 0,93.
Решение.
Составим разность 4/5 - 0,93 и найдем значение этой разности:
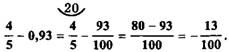
Разность отрицательна, поэтому 4/5<0,93.
Ответ: 4/5<0,93.
Сравнение действительных чисел






