Связь между радианной и градусной мерами угла
Поскольку длина всей окружности равна  , то полный угол составляет
, то полный угол составляет  радиан, т. к.
радиан, т. к.  . Поскольку полный угол равен 360° , то
. Поскольку полный угол равен 360° , то  .
.
Отсюда 1 радиан =  (57 градусов, 17 минут, 45 секунд).
(57 градусов, 17 минут, 45 секунд).
Таким образом, из соотношений  можно переходить от градусов к радианам и наоборот.
можно переходить от градусов к радианам и наоборот.
Пример 1. а) Выразить в радианах угол в 30°;
б) выразить в градусах угол в 2 радиана.
Решение.
а) 
б) 
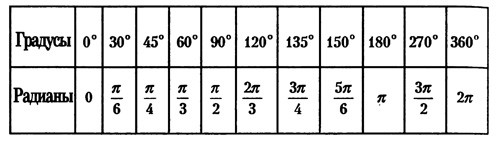
Приведем таблицу перехода от градусов к радианам наиболее распространенных углов (табл. 1).
Таблица 1
Соответствие между градусами и радианами