Тригонометрия. Углы и их измерения

Угол — это геометрическая фигура, образованная двумя лучами, исходящими из одной точки, называемой вершиной угла (рис.1).

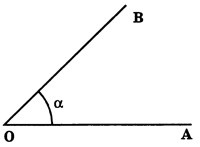
Слово «угол» заменяют символом $\angle$: $\angle AOB=\angle BOA=\angle \alpha$. Часто символ $\angle$ опускают и пишут просто $\alpha$, т.е. $\alpha =\angle \alpha$.
Угол можно рассматривать как фигуру, образованную вращением луча вокруг своей начальной точки O. Луч можно вращать вокруг своей начальной точки в двух направлениях: по часовой стрелке и против часовой стрелки. Направление вращения против часовой стрелки условились называть положительным, а по часовой стрелке — отрицательным. Соответственно этому углы и дуги, полученные вращением луча против часовой стрелки, считаются положительными, а углы и дуги, полученные вращением луча по часовой стрелке, считаются отрицательными (рис. 2).

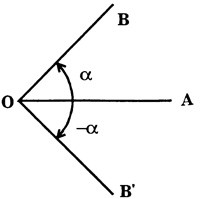
Если стороны угла образуют прямую, то такой угол называется развернутым. Если луч сделает полный оборот вокруг своей начальной точки, то полученный угол называется полным.
Оси абсцисс (Ох) и ординат (Оу) делят полный угол (окружность) на четыре четверти (I—IV), или четыре квадранта (рис. 3).

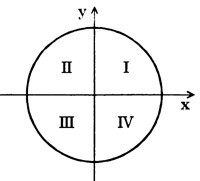
Углы измеряются в градусах и радианах. Угол в 1 градус — это угол, который опишет луч, совершив 1/360 часть полного оборота вокруг своей начальной точки продев часовой стрелки (обозначение 1°). 1/60 часть градуса называется минутой (обозначается ${1}'$). 1/60 часть минуты называется секундой (обозначается ${1}''$).
Центральным углом в окружности называется угол, вершина которого находится в ее центре.
Угол в 1 радиан — это центральный угол, опирающийся на такую дугу окружности, длина которой равна радиусу этой окружности (рис. 4).

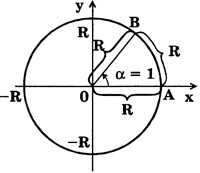
Слово «радиан» обычно не пишут. Таким образом, если

$$\left | \breve{AB} \right |=R,\; \left | OA \right |=\left | OB \right |=R,$$

то $\angle AOB=\angle \alpha=1$, т. е. угол $\alpha$ равен одному радиану.