Примеры решения рациональных неравенств методом интервалов

Примеры решения рациональных неравенств методом интервалов
Пример 1. Решить неравенство $(x-1)(x-3)>0$.
Решение. Многочлен $f(x)=(x-1)(x-3)$ обращается в нуль в точках $x=1,\; x=3$. Эти точки разбивают координатную прямую на промежутки $(-\propto ;1),\; (1;3),\; (3;+\propto)$, внутри каждого из которых функция $f(x)$ сохраняет знак. Так как в промежутке $(3;+\propto)$, сомножители $(x-1),(x-3)$ положительны, то и их произведение положительно, т. е. $f(x)>0$. Отметим промежуток $(3;+\propto)$ знаком « + ». Далее знаки в промежутках чередуются. Проводим через отмеченные точки «кривую знаков»(рис. 1).

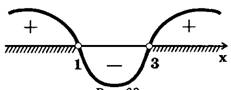
Иллюстрацию с помощью «кривой знаков» понимаем так: на тех промежутках, где «кривая знаков» проходит выше координатной прямой (где ставится знак « + »), выполняется неравенство $f(x)>0$; на тех промежутках, где кривая проходит ниже прямой (где знак «-»), выполняется неравенство $f(x)<0$. В результате получаем, что решение исходного неравенства есть объединение промежутков: $(-\propto ;1),\; (3;+\propto)$. Это множество на рис.1 заштриховано. Ответ: $x\in (-\propto ;1)\bigcup (3;+\propto)$ .
Пример 2. Решить неравенство $(2-x)(x+1)(x-4)\leq 0$.
Решение. Наносим на числовую ось точки х=2; х=—1; х=4 (рис.2). Поскольку решаем нестрогое неравенство, то точки $x=2;\; x=-1;\; x=4$ окрашиваем в темный цвет (ставим темные кружки). Взяв, например, в интервале $(-1;2)$ точку $x=0$, определяем знаковой части исходного неравенства: $(2-0)(0+1)(0-4)=-8<0$. Отсюда при $x\in \left[-1;2 \right]$ имеем $(2-x)(x+1)(x-4)\leq 0$. Проведя «кривую знаков», определяем знак левой части исходного неравенства в каждом из промежутков. Множество, дающее решение исходного неравенства, есть объединение промежутков: $\left[-1;2 \right]$, $\left[4;+\propto \right)$. Это множество заштриховано на рис.2.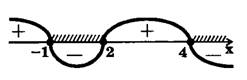

Ответ: $x\in \left(-1;2 \right)\bigcup \left[4;+\propto \right)$.
Пример 3. Решить неравенство $\frac{3x}{(x+2)(x-4)}<0.$

Решение. Корнями уравнений $3x=0,\; x+2=0,\; x-4=0$ являются числа $x=0, x=-2, x=4$. Наносим эти числа на прямую (рис.3) и определяем знак левой части неравенства, т. е. знак функции $f(x)=\frac{3x}{(x+2)(x-4)}$ на одном из интервалов.

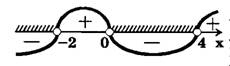
В частности, взяв $x=5$, получаем $f(5)=\frac{3\cdot 5}{(5+2)(5-4)}=\frac{15}{7}>0$. Отсюда при $x>4\; f(x)>0$. Проведя «кривую знаков», определяем знак $f(x)$ в каждом из интервалов. Множество, дающее решение исходного неравенства, заштриховано на рис.2. Это множество — объединение промежутков $(-\propto ;-2),\; (0;4)$. Точки $x=-2,\; x=0,\; x=4$ «выкалываются», т. е. представляются светлыми кружками.
Ответ: $x\in (-\propto ;-2)\bigcup (0;4)$.
Пример 4. Решить неравенство $\frac{(x+1)(x-2)}{(4-x)(x+2)}\geq 0$.
Решение. Корнями уравнений $x+1=0,\; x-2=0,\; 4-x=0,\; x+2=0$ являются числа $x=-1, \;x=2,\; x=4,\; x=-2$. Наносим эти числа на числовую ось. Точки $x=-1, \;x=2$ отмечаем темными кружками, т. к. решается нестрогое неравенство и выражения $(x+1)$ и $(x-2)$ находятся в числителе. Точки $x=4, \;x=-2$ отмечаем светлыми кружками, т. к. хотя решается и нестрогое неравенство, но эти точки ($x=4, \;x=-2$) не входят в область определения функции $f(x)=\frac{(x+1)(x-2)}{(4-x)(x+2)}$. Проведя «кривую знаков», определяем знак $f(x)$ в каждом из интервалов (рис.4). Множество, дающее решение исходного неравенства, заштриховано на рис.4

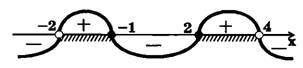
Ответ: $x\in (-2;1]\bigcup [2;4)$.
Пример 5. Решить неравенство $\frac{1}{2x}>3$.
Решение. Преобразуем исходное неравенство следующим образом:

$$\frac{1}{2x}>3\Leftrightarrow \frac{1}{2x}-3>0\Leftrightarrow \frac{1-6x}{2x}>0.$$

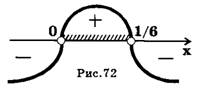
Применяя «кривую знаков» (рис.5), получаем, что исходное неравенство выполняется при $x\in \left(0;\frac{1}{6} \right)$. Это множество заштриховано на рис.5.
Ответ: $x\in \left(0;\frac{1}{6} \right)$.
Пример 6. Решить неравенство $\frac{x^{2}-3x+2}{x^{2}+3x+2}\geq 1$.
Решение. Преобразуем исходное неравенство:

$$\frac{x^{2}-3x+2}{x^{2}+3x+2}\geq 1 \Leftrightarrow \frac{x^{2}-3x+2}{x^{2}+3x+2}-1 \geq 0 \Leftrightarrow \frac{x^{2}-3x+2-x^{2}-3x-2}{x^{2}+3x+2}\geq 0 \Leftrightarrow$$

$$\Leftrightarrow \frac{-6x}{(x+1)(x+2)}\geq 0 \Leftrightarrow \frac{6x}{(x+1)(x+2)}\leq 0.$$

В процессе преобразований мы учли, что $x^{2}+3x+2=(x+1)(x+2)$, а также тот факт, что при умножении на отрицательное число знак неравенства изменяется на противоположный. Применяя «кривую знаков» (рис. 6), получим, что неравенство $\frac{6x}{(x+1)(x+2)}\leq 0$, равносильное исходному, выполняется ,при $x\in (-\propto ;-2)\bigcup (-1;0]$. Это множество заштриховано на рис.6.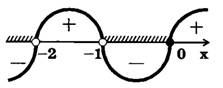

Ответ: $x\in (-\propto ;-2)\bigcup (-1;0]$.