Решение рациональных неравенств методом интервалов

Решение рациональных неравенств методом интервалов
Неравенства вида $P_{n}(x)>0 \left(P_{n}(x)<0,\: P_{n}(x)\geq 0,\: P_{n}(x)\leq 0 \right)$, $\frac{P_{n}(x)}{Q_{m}(x)}>0 \left(\frac{P_{n}(x)}{Q_{m}(x)}<0,\: \frac{P_{n}(x)}{Q_{m}(x)}\geq 0,\: \frac{P_{n}(x)}{Q_{m}(x)}\leq 0 \right),$ где $P_{n}(x),Q_{m}(x)$ — многочлены соответственно степеней n и m, т. е.
$P_{n}(x)=a_{0}x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+...+a_{n-1}x+a_{n},$
$Q_{m}(x)=b_{0}x^{m}+b_{1}x^{m-1}+b_{2}x^{m-2}+...+b_{m-1}x+b_{m},$
обычно решают методом интервалов (методом промежутков). Этот метод удобен, например, для решения неравенств следующего вида:

$$x(x+1)\geq 0,\; \frac{3x}{x-3}<0,\; (x-1)(x-3)(x+5)\leq 0,\; \frac{x^{2}+5x+6}{x^{2}-5x-6}\geq 0,\; \frac{(x-1)(x-3)(x-5)}{(x+1)(x+3)}<0$$

В основе метода интервалов лежит следующее свойство двучлена $x-\alpha$: точка $x=\alpha$ делит числовую ось на две части — справа от точки $\alpha$ двучлен $(x-\alpha)>0$ а слева от точки $\alpha$ $(x-\alpha)<0$ (рис.1).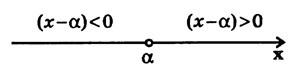

Пусть требуется решить неравенство $(x-\alpha _{1})(x-\alpha _{2})...(x-\alpha _{n})>0$, где $\alpha _{1},\alpha _{2},...,\alpha _{n}$ — фиксированные числа, среди которых нет равных, причем такие, что $\alpha _{1}<\alpha _{2}<...<\alpha _{n}$. Для решения неравенства $(x-\alpha _{1})(x-\alpha _{2})...(x-\alpha _{n})>0$ методом интервалов поступают следующим образом: на числовую ось наносят числа $\alpha _{1},\alpha _{2},...,\alpha _{n}$; в промежутке справа от наибольшего из них, т. е. числа $\alpha _{n}$, ставят знак «плюс», в следующем за ним справа налево интервале ставят знак «минус», затем — знак «плюс», затем знак «минус» и т. д. Тогда множество всех решений неравенства $(x-\alpha _{1})(x-\alpha _{2})...(x-\alpha _{n})>0$ будет объединение всех промежутков, в которых поставлен знак «плюс», а множество решений неравенства $(x-\alpha _{1})(x-\alpha _{2})...(x-\alpha _{n})<0$ будет объединение всех промежутков, в которых поставлен знак «минус».

Замечание 1. На практике среди двучленов встречаются выражения $(\alpha _{i}-x)$, в этом случае справа от наибольшего числа $x=\alpha _{n}$ уже не обязательно будет знак «плюс». Поэтому неравенства, где в левой части встречаются двучлены вида $(\alpha _{i}-x)$, лучше всего решать так: найти знак левой части выражения в каком-то одном из интервалов, не обязательно крайнем справа, а дальше в соседних интервалах будут противоположные знаки.
Замечание 2. Изменение знаков левой части неравенства удобно иллюстрировать с помощью волнообразной кривой (которую называют «кривой знаков»), проведенной через отмеченные точки и лежащей выше или ниже числовой оси в соответствии со знаком неравенства в рассматриваемом промежутке.
Замечание 3. Приведенные выше рассуждения справедливы и для неравенств вида $f(x)<0,\: f(x)\geq 0,\: f(x)\leq 0$, где $f(x)$ имеет вид $f(x)=\frac{(x-a_{1})(x-a_{2})...(x-a_{n})}{(x-b_{1})(x-b_{2})...(x-b_{k})},$ при этом числа $a_{1},a_{2},...,a_{n},b_{1},b_{2},...,b_{k}$ попарно различны. При этом изменение знаков функции $f(x)$ иллюстрируется с помощью «кривой знаков».