Всякое число, кроме единицы, которое делится только на 1 и само на себя, называется простым. Таким образом, простое число имеет только два делителя: само это число и единицу. Число, которое делится не только на единицу и само на себя, но еще и на другие числа, называется составным. Составное число имеет более двух делителей.
Число 1 (единица) не относится ни к простым, ни к составным числам.
Любое составное натуральное число можно разложить на простые множители, и только одним способом.
При разложении чисел на простые множители обычно записывают столбик, при этом делитель располагается справа от вертикальной черты, а частное записывается под делимым. Так, для чисел 300, 630 имеем:
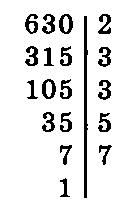
Если в разложении числа на простые множители один и тот же множитель а встречается n раз, то записывают коротко
Выражение aⁿ называется степенью, а — основанием степени, n — показателем степени. Отсюда
Разложение натурального числа на произведение степеней простых сомножителей (основная теорема арифметики) имеет вид:
где N — любое натуральное число, большее 1;
— попарно различные простые числа; αᵢ — натуральные числа (i = 1, 2,..., m-1,m).
Математика "с нуля". Урок 20. Разложение чисел на простые множители
