Построение графиков тригонометрических функций с помощью преобразований. Решения упражнений. Учимся решать задачи по тригонометрии. Видеоурок №40
Пример 1. Построить график функции  .
.
Решение.
Подвергнем график функции  параллельному переносу вдоль оси абсцисс на
параллельному переносу вдоль оси абсцисс на  единиц в положительном направлении. Получим график
единиц в положительном направлении. Получим график  . Затем ту часть графика, которая лежит в полуплоскости
. Затем ту часть графика, которая лежит в полуплоскости  , симметрично отразим относительно оси ординат. Объединение симметричных частей и будет искомым графиком .
, симметрично отразим относительно оси ординат. Объединение симметричных частей и будет искомым графиком .
Замечание. Широко распространена следующая ошибка: вначале построить график функции  . Затем считать, что искомый график получается в результате параллельного переноса графика
. Затем считать, что искомый график получается в результате параллельного переноса графика  вдоль оси абсцисс в положительном направлении на
вдоль оси абсцисс в положительном направлении на  единицы. На самом деле такие преобразования приведут к графику функции
единицы. На самом деле такие преобразования приведут к графику функции  .
.
Пример 2. Построить график функции  .
.
Решение.
Проведем следующие преобразования:
1) 
2)  — сжатие к оси ординат в два раза;
— сжатие к оси ординат в два раза;
3)  — параллельный перенос вдоль оси абсцисс в положительном направлении на
— параллельный перенос вдоль оси абсцисс в положительном направлении на  единиц.
единиц.
Правила преобразований графика функции 
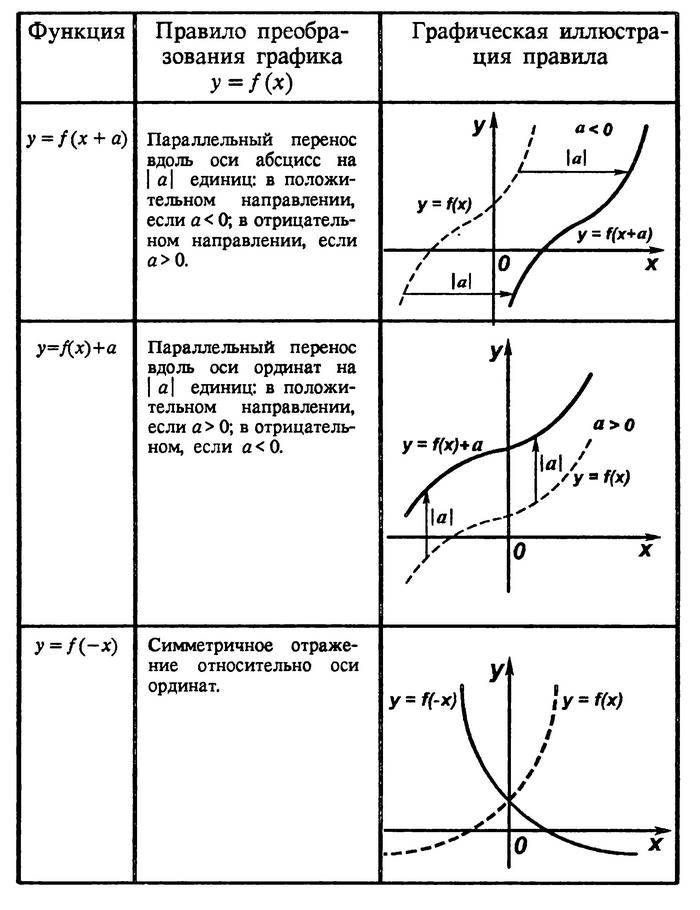
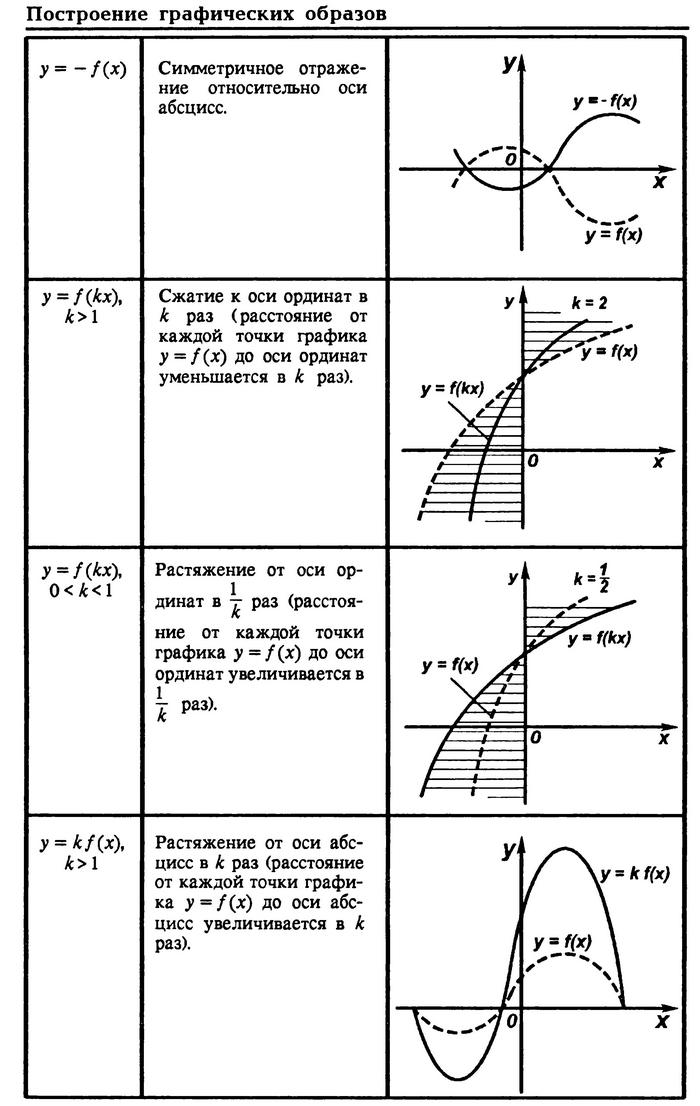
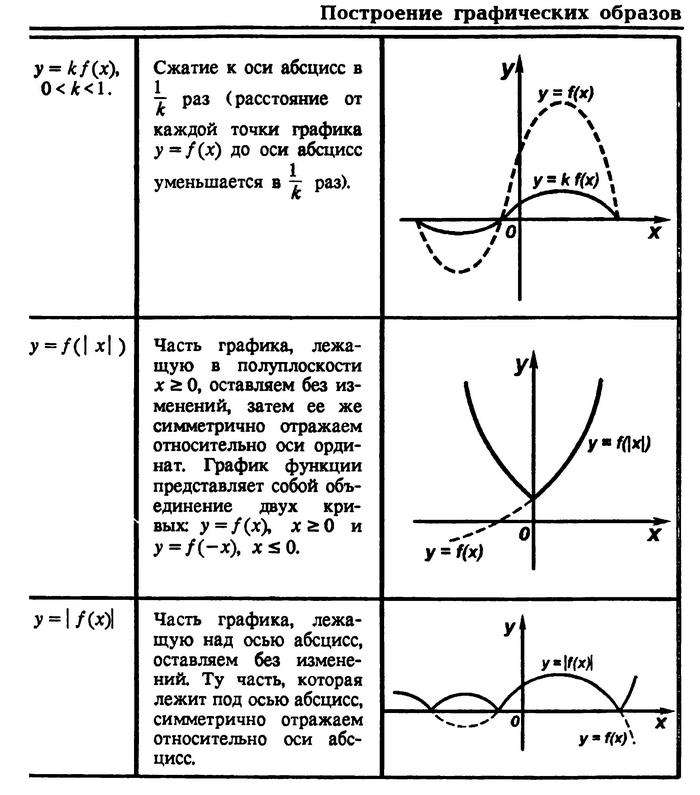
Полный урок смотрите в следующем видео:
Домашнее задание:
1. Постройте график функции:
1) 
2) 
3) 
2. Постройте график функции:
1) 
2) 
3) 
3. Постройте график функции:
1) 
2) 
3) 
4) 
5) 
4. Постройте график функции:
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
5. Постройте график функции:
1) 
2) 
3) 








