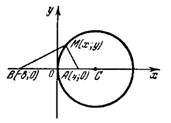
Задача № 1. Даны: точка D(4; 3) и окружность радиуса г= 1 с центром в точке С(2; 4).
Требуется найти такую точку М, чтобы длина касательной, проведенной из нее к окружности, была равна расстоянию точки М до точки D (рис.1).
Решение. Пусть искомая точка есть М (х, у) (рис.1).
Согласно условия MB=MD, где точка В есть точка касания прямой к окружности. Тогда треугольник МВС - прямоугольный, из которого находим, что MB![]()
но МС²=(х-2)²+ (y-4)², а ВС=г=1.
Имеем
![]()
Расстояние точки М от точки D равно:
![]()
Имеем уравнение
![]()
Возводя в квадрат обе части уравнения, найдем
После преобразования получим:
Следовательно, точек, удовлетворяющих заданному условию, будет бесчисленное множество. Они образуют прямую, уравнение которой найдено.
Задача № 2. Составить уравнение геометрического места точек, одинаково удаленных от оси Оу и от точки F(4; 0).
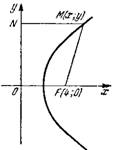
Решение. Пусть точка М (х,у) лежит на искомом геометрическом месте точек (hbc.2). Тогда согласно условию задачи MF = MN,
![]()
В силу равенства MF = MN имеем:
![]()
или
и окончательно
Искомое геометрическое место точек есть парабола, симметричная относительно оси Ох и с фокусом в точке (4; 0).
Покажем, что координаты точки, не принадлежащей нашему геометрическому месту, т. е. параболе, не удовлетворяют найденному уравнению
Предположим, что точка М (х, у) не принадлежит искомому геометрическому месту. Тогда либо MF>MN, либо MF
После возведения в квадрат, раскрытия скобок и переноса всех членов влево, получим: у2—8х+16>0.
Следовательно, точка М (х, у) не удовлетворяет уравнению геометрического места
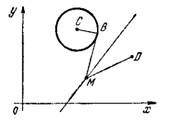
Для случая MF
Решение. Пусть точка М(х,у) лежит на искомой траектории. Тогда, согласно условию 2МA = МВ.
Расстояние ![]()
расстояние ![]()
В силу равенства 2МА=МВ, имеем:
![]()
Возводим правую и левую часть равенства в квадрат, получаем
![]()
После преобразования получим
Искомая траектория точки М—окружность (рис.3)