Предел функции многих переменных. Непрерывность. Практикум по математическому анализу. Урок 100

Предел функции многих переменных. Непрерывность
Число $A$ называется пределом функции $f(M)$ в точке $M_{0}$:

$$\displaystyle \underset{M \to M_{0}}{\lim }f(M)=A,$$

если абсолютное значение разности $f(M)-f(M_{0})$ будет меньше любого заранее данного положительного числа $\varepsilon$, когда расстояние $MM_{0}$ меньше некоторого положительного числа $\delta$ (зависящего от $\varepsilon$).
Функция $f(M)$ называется непрерывной в точке $M_{0}$, если

$$\displaystyle \underset{M \to M_{0}}{\lim }f(M)=f(M_{0}).$$

Для непрерывности функции $f(M)$ в точке $M_{0}$ необходимо выполнение следующих условий:
1) $f(M)$ должна быть определена в точке $M_{0}$ и вблизи этой точки;
2) $f(M)$ должна иметь предел, когда точка $\displaystyle M \to M_{0}$ произвольным способом;
3) этот предел должен быть равен $\displaystyle f(M_{0})$.
Функция $f(M)$, непрерывная в каждой точке некоторой области $D$, называется непрерывной в этой области.

Пример 1. Найти пределы:
1) $\displaystyle \underset{\begin{matrix} x \to 3\\ y \to 0 \end{matrix}}{\lim }\frac{tg(xy)}{y};$
2) $\displaystyle \underset{\begin{matrix} x \to 0\\ y \to 0 \end{matrix}}{\lim }\frac{x}{x+y}.$

Решение. Убедившись, что функция не определена в предельной точке, делаем преобразования

1) $\displaystyle \underset{\begin{matrix} x \to 3\\ y \to 0 \end{matrix}}{\lim }\frac{tg(xy)}{y}=\lim x\cdot \lim \frac{\textrm{tg}(xy)}{xy}=3\cdot 1=3,$ так как $\displaystyle \underset{\alpha \to 0}{\lim }\frac{\textrm{tg} \alpha}{\alpha}=1.$

2) $\displaystyle \underset{\begin{matrix} x \to 0\\ y \to 0 \end{matrix}}{\lim }\frac{x}{x+y}=\lim \frac{1}{1+\frac{y}{x}}$ не существует, ибо отношение $\displaystyle \frac{y}{x}$ не имеет предела при произвольном стремлении точки $M(x,y)$ к точке $M_{0}(0;0)$. Так, если $M \to M_{0}$ вдоль различных прямых $y=kx$, то $\displaystyle \frac{y}{x}=k$, т. е. зависит от углового коэффициента прямой, по которой движется точка $M$.

Пример 2. В каких случаях функция многих переменных $f(M)$ будет разрывна в точке $M_{0}$? Поясните их примерами.

Решение. 1) Функция $f(M)$ будет разрывна в точке $M_{0}$, если она определена вблизи этой точки, но не определена в самой точке $M_{0}$.

Например, функция $\displaystyle z=\frac{1}{\sqrt{x^{2}+3y^{2}}}$ определена на всей плоскости $xOy$, но не определена в точке $\displaystyle M_{0}(0;0)$, поэтому в этой точке функция разрывна. Во всех других точках числовой плоскости она непрерывна.

2) Функция $f(M)$ будет разрывна в точке $M_{0}$, если она определена вблизи этой точки и в самой точке, но не имеет предела, когда точка $M \to M_{0}$.
Например, функция

$$\displaystyle u=\left\{\begin{matrix} \sin \frac{1}{x^{2}+y^{2}},\: x\neq 0,y\neq 0\\ 3,\: x=y=0 \end{matrix}\right.$$

разрывна в точке $\displaystyle M_{0}(0;0)$, так как она определена вблизи этой точки и в самой точке (на всей плоскости $xOy$), но не имеет предела при $M \to M_{0}$. В остальных точках плоскости $xOy$ она непрерывна.

3) Функция $f(M)$ будет разрывна в точке $M_{0}$, если она определена вблизи этой точки и в самой точке, но $\displaystyle \underset{M \to M_{0}}{\lim }f(M)\neq f(M_{0})$.

Например, функция

$$\displaystyle z=\left\{\begin{matrix} 5-x-y,\: x\neq 1,y\neq 2\\ 1,\: x=1,y=2 \end{matrix}\right.$$

разрывна в точке $\displaystyle M_{0}(1;2)$, ибо она определена вблизи этой точки и в самой точке, но ее предел при $\displaystyle M \to M_{0}$ не совпадает с частным значением в точке $M_{0}$; $\displaystyle \underset{M \to M_{0}}{\lim }z=2\neq z(M_{0})=1.$

Графиком этой функции является вся плоскость $\displaystyle z=5-x-y$ без точки $\displaystyle P(1;2;2)$, вместо которой графику принадлежит точка $\displaystyle Q(1;2;1)$ (рис. 1).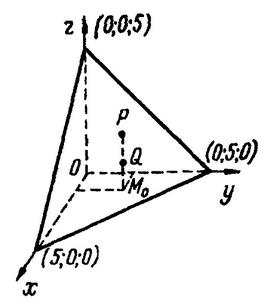

Функция двух переменных $z=f(x,y)$ может иметь множество точек разрыва; если они составляют линию, то она называется линией разрыва функции.

Например, функция $\displaystyle z=\frac{1}{1-x^{2}-y^{2}}$ разрывна в каждой точке окружности $\displaystyle x^{2}+y^{2}=1$. Эта окружность есть линия разрыва данной функции.