Пример 3. Найти координаты центра кривизны и построить кривую и круг кривизны кривой:
1)  в ее вершине;
в ее вершине;
2)  в точке, где
в точке, где  .
.
Решение. 1) Данное уравнение определяет параболу, ось которой параллельна оси  . Найдем ее вершину как точку, где касательная параллельна оси
. Найдем ее вершину как точку, где касательная параллельна оси  , т. е. где
, т. е. где  :
:
 при
при 
Далее по формулам


находим координаты центра кривизны
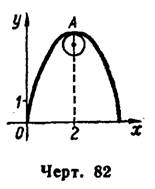
 данной параболы в ее вершине (2; 4)
данной параболы в ее вершине (2; 4)
и строим параболу и круг кривизны в ее вершине (рис. 82).
2) Находим производные
 , их значения при
, их значения при  :
:
и по формулам (2) координаты центра кривизны

Затем строим данную циклоиду, ее точку
 , где
, где , найденный центр кривизны
, найденный центр кривизны  и круг кривизны (рис. 83).
и круг кривизны (рис. 83).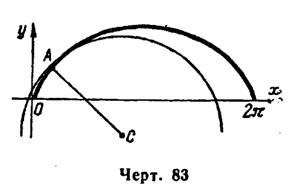
Пример 4. В каких точках параболы
 радиус кривизны равен единице?
радиус кривизны равен единице?Решение. Находим производные
 и по формуле (1)
и по формуле (1)![\displaystyle K=\frac{\left | y'' \right |}{\left [ 1+(y')^{2}\right ]^{\frac{3}{2}}}=\frac{\left | \dot{x}\ddot{y}-\dot{y}\ddot{x} \right |}{(\dot{x}^{2}+\dot{y}^{2})^{\frac{3}{2}}}, \; \; \; \; (1)](https://math-helper.net/wp-content/plugins/latex/cache/tex_ccb926d5288bc7fc10b1908902ef4107.gif)
радиус кривизны параболы в любой ее точке с абсциссой
 :
:
Полагая
 , получим абсциссы искомых точек
, получим абсциссы искомых точек
Пример 5. В какой точке кривая
 имеет наибольшую кривизну?
имеет наибольшую кривизну?Решение. Находим производные
 и кривизну данной кривой в любой точке:
и кривизну данной кривой в любой точке:
Далее ищем наибольшее значение функции
 , которая определена и непрерывна на всей числовой оси:
, которая определена и непрерывна на всей числовой оси:  при
при 
т.е. в единственной точке  . Определяя знаки
. Определяя знаки  слева и справа от этой критической точки:
слева и справа от этой критической точки:  0, \: K'(0)<0" />, устанавливаем, что она является точкой максимума функции
0, \: K'(0)<0" />, устанавливаем, что она является точкой максимума функции  . Поскольку
. Поскольку  есть единственная точка экстремума непрерывной функции
есть единственная точка экстремума непрерывной функции  во всем интервале
во всем интервале  , то в этой точке она достигает и своего наибольшего значения. Следовательно, искомая точка есть
, то в этой точке она достигает и своего наибольшего значения. Следовательно, искомая точка есть  . (Ордината этой точки вычислена из данного уравнения кривой по известной ее абсциссе.)
. (Ордината этой точки вычислена из данного уравнения кривой по известной ее абсциссе.)
Пример 6. Найти уравнение эволюты кривой и построить кривую и ее эволюту:
1)  ; 2)
; 2)  .
.
Решение. 1) Из данного уравнения параболы находим производные:  и по формулам (2) находим координаты любой точки на ее эволюте:
и по формулам (2) находим координаты любой точки на ее эволюте:


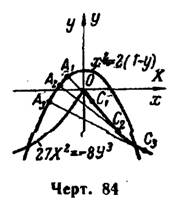
Это параметрические уравнения эволюты. Исключая из них параметр
 , получим
, получим  — уравнение полукубической параболы. Данная парабола и найденная ее эволюта изображены на рис. 84.
— уравнение полукубической параболы. Данная парабола и найденная ее эволюта изображены на рис. 84.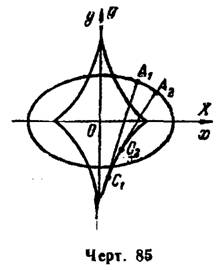
2) Из уравнений эллипса найдем производные
 и по формулам (2) получим, после упрощений, параметрические уравнения эволюты эллипса
и по формулам (2) получим, после упрощений, параметрические уравнения эволюты эллипса  где
где 
Эллипс и его эволюта построены на рис. 85.







