1. Гипербола
Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, равная 2а (рис.1). Каноническое уравнение гиперболы имеет вид
![]()
Координаты фокусов гиперболы: F(c;0) и F₁(-c;0). Расстояние между фокусами равно 2с.
Точки пересечения гиперболы с осью абсцисс А(а;0) и A₁(—а;0) называются действительными вершинами.
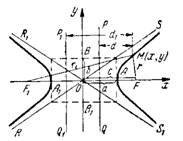
Отрезок АА₁ = 2а называется действительной осью гиперболы. Точки В (0;b) и В₁(0;—b) называются мнимыми вершинами гиперболы, а отрезок ВВ₁ = 2b называется мнимой осью гиперболы.
Эксцентриситет гиперболы
![]()
Расстояния r и r₁ точки М(x;у) гиперболы до ее фокусов называются фокальными радиусами этой точки и определяются формулами:
![]()
если точка М лежит на правой ветви;
![]()
если точка М лежит на левой ветви.
Две прямые PQ и P₁Q₁ параллельные мнимой оси гиперболы и
отстоящие от нее на расстоянии a/e, называются директрисами гиперболы. Их уравнения:
![]()
или
![]()
Отношение расстояний любой точки гиперболы до фокуса и соответствующей директрисы есть величина постоянная, равная эксцентриситету гиперболы
![]()
Прямые RS и R₁S₁ определяемые уравнениями
![]()
называются асимптотами гиперболы.
Уравнение гиперболы с осями, параллельными координатным осям, имеет вид:
![]()
где x₀, у₀ — координаты центра гиперболы. Две гиперболы, выраженные уравнениями
![]()
![]()
называются сопряженными (рис.3). Они имеют общие асимптоты.
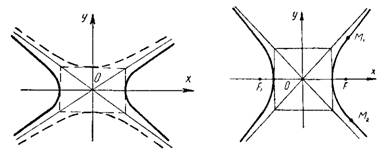
Рис. 3. Рис. 4.
Если оси гиперболы равны, т. е. a = b, то гипербола называется равнобочной или равносторонней (рис.4). Ее уравнение имеет вид
![]()
ее асимптотами служат биссектрисы координатных углов. Если за оси координат принять асимптоты равносторонней гиперболы, то ее уравнение примет вид
![]()
2. Парабола
Параболой называется геометрическое место точек плоскости, равноудаленных oт данной точки — фокуса и данной прямой — директрисы (рис.5).
Каноническое уравнение параболы имеет вид
![]()
где Р — есть расстояние от фокуса до директрисы. Вершина параболы находится в начале координат, осью симметрии служит ось абсцисс.
Координаты фокуса F(p/2;0). Уравнение директрисы PQ параболы имеет вид
![]()
Фокальный радиус точки М(х;у) параболы равен:
![]()
Эксцентриситет параболы считается равным единице, е=1. Если осью симметрии параболы служит ось ординат (рис.6). то уравнение параболы имеет вид:
![]()
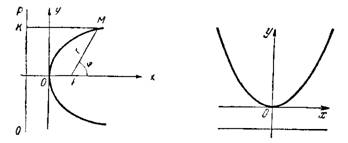
Рис. 3. Рис. 4.
Уравнение директрисы в этом случае
![]()
Уравнение параболы с осью симметрии, параллельной одной из координатных осей, имеет вид:
![]()
или
![]()
где (x₀; y₀) — координаты вершины параболы.
3. Уравнения эллипса, гиперболы и параболы в полярных координатах
Уравнения эллипса, гиперболы и параболы в полярных координатах имеют один и тот же вид:
![]()
где е — эксцентриситет кривой.
Если е<1, то кривая, определяемая уравнением (27), есть эллипс; если е>1, то кривая — гипербола и если е=1, то кривая — парабола.
р — фокальный параметр для эллипса и гиперболы находится по формуле
![]()
Для параболы р имеет то же значение, что и в уравнении
При этом полюс расположен для эллипса в левом фокусе, для гиперболы — в правом фокусе.







