Некоторые приложения определителей к аналитической геометрии
1. Площадь треугольника с вершинами в точках 

2. Условие, при котором три точки  лежат на одной прямой
лежат на одной прямой

3. Уравнение прямой, проходящей через две данные точки 

4. Условие, при котором три прямые  пересекаются в одной точке:
пересекаются в одной точке:

Пример 1. Найти площадь четырехугольника с вершинами в точках А (1; 2), В (—2; 1), С (—3; —4), D (5; —7).
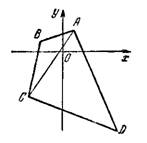
Решение. Площадь четырехугольника равна сумме площадей треугольников ABC и ACD.



Ответ: 23 кв.ед.
Пример 2. На прямой, проходящей через точку M(-3; 8) и N(5; —1), найти точку, абсцисса которой равнялась бы 1.
Решение. Воспользуемся условием того, что три точки лежат на одной прямой.


Координаты искомой точки Р(1; у):


Ответ: P(1; 3,5).







