Непрерывность и точки разрыва функции. Примеры. Практикум по математическому анализу. Урок 23

Пример 1. Для каждой из следующих функций найти точки разрыва, если они существуют, найти скачок функции в каждой точке разрыва и построить график:
1) $\displaystyle f(x)=\left\{\begin{matrix} -\frac{1}{2}x^{2},\: if\: x\leq 2,\\ x,\: if\: x>2; \end{matrix}\right.$
2) $\displaystyle \varphi (x)=\left\{\begin{matrix} 2\sqrt{x},\: if\: 0\leq x\leq 1,\\ 4-2x,\: if\: 1<x<2,5,\\ 2x-7,\: if\: 2,5\leq x<+\infty ; \end{matrix}\right.$

3) $\displaystyle F(x)=\left\{\begin{matrix} 2x+5,\: if\: -\infty <x<-1,\\ \frac{1}{x},\: if\: -1\leq x<+\infty . \end{matrix}\right.$ Решение. 1) Функция $f(x)$ определена на всей числовой оси. Но из этого не следует, xто она и непрерывна на всей числовой оси, так как эта функция неэлементарная; она задана двумя различными формулами для различных интервалов изменения аргумента $x$ и может иметь разрыв в точке $x=2$, где меняется ее аналитическое выражение.
Исследуя точку находим односторонние пределы функции при стремлении аргумента к этой точке слева и справа:
$\displaystyle \underset{x \to 2-0}{\textrm{lim}}f(x)=\underset{x \to 2-0}{\textrm{lim}}\left ( -\frac{1}{2} x^{2}\right )=-2$,
так как слева от точки $x=2$ функция $\displaystyle f(x)=-\frac{1}{2}x^{2}$;
$\displaystyle \underset{x \to 2+0}{\textrm{lim}}f(x)=\underset{x \to 2+0}{\textrm{lim}}x=2$,
так как справа от точки $x=2$ функция $\displaystyle f(x)=x$.
Левый и правый пределы функции конечны, но не равны между собой. Поэтому, вследствие невыполнения 2-го условия непрерывности, в точке $x=2$ функция имеет разрыв (конечный).
В этой точке разрыва функция имеет конечный скачок:
$\displaystyle \underset{x \to 2+0}{\textrm{lim}}f(x)-\underset{x \to 2-0}{\textrm{lim}}f(x)=2-(-2)=4.$
Во всех остальных точках числовой оси функция $f(x)$ непрерывна, так как обе формулы, которыми она задана, определяют собой элементарные непрерывные функции.

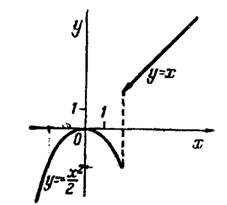
Рис.1

График этой функции показан на рис.1.
2) Неэлементарная функция $\displaystyle \varphi (x)$ определена для всех значений $\displaystyle x\geq 0$. Она может иметь разрыв в точках $x=1$ и $x=2,5$, где меняется ее аналитическое выражение. Во всех остальных точках своей области определения функция $\displaystyle \varphi (x)$ непрерывна, поскольку каждая из формул, которыми она задана, определяет собой элементарную функцию, непрерывную в своем интервале изменения аргумента $x$.
Исследуем точки $x=1$ и $x=2,5$:
a) $\displaystyle \underset{x \to 1-0}{\textrm{lim}}\varphi (x)=\underset{x \to 1-0}{\textrm{lim}}2\sqrt{x}=2;\: \underset{x \to 1+0}{\textrm{lim}}\varphi (x)=\underset{x \to 1+0}{\textrm{lim}}(4-2x)=2.$
Согласно условию значение функции $\displaystyle \varphi (x)$ в точке $x=1$ определяется первой формулой
$\displaystyle \varphi (1)=2\sqrt{1}=2.$
Следовательно, в точке $x=1$ выполняются все условия непрерывности: функция определена в окрестности точки $x=1$ и
$\displaystyle \underset{x \to 1-0}{\textrm{lim}}\varphi (x)=\underset{x \to 1+0}{\textrm{lim}}\varphi (x)=\varphi (1).$
Поэтому в точке $x=1$ функция $\displaystyle \varphi (x)$ непрерывна.
б) $\displaystyle \underset{x \to 2,5-0}{\textrm{lim}}\varphi (x)=\underset{x \to 2,5-0}{\textrm{lim}}(4-2x)=-1;\; \underset{x \to 2,5+0}{\textrm{lim}}\varphi (x)=\underset{x \to 2,5+0}{\textrm{lim}}(2x-7)=-2.$
Здесь левый и правый пределы функции конечны, но не одинаковы, т. е. не выполняется 2-е условие непрерывности.

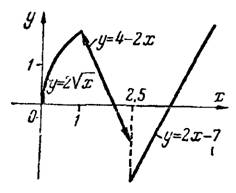
Рис.2

Поэтому в точке $x=2,5$ функция имеет разрыв (конечный), рис.2. Скачок функции в точке разрыва конечный:
$\displaystyle \underset{x \to 2,5+0}{\textrm{lim}}\varphi (x)-\underset{x \to 2,5-0}{\textrm{lim}}\varphi (x)=-2-(-1)=-1.$
3) Неэлементарная функция $F(x)$ определена на всей числовой оси, кроме точки $x=0$. Это значит, что в точке $x=0$ функция разрывна. Исследуем эту точку:
$\displaystyle \underset{x \to -0}{\textrm{lim}}F(x)=\underset{x \to -0}{\textrm{lim}}\frac{1}{x}=-\infty,\; \underset{x \to +0}{\textrm{lim}}F(x)=\underset{x \to +0}{\textrm{lim}}\frac{1}{x}=+\infty.$
Следовательно, в точке $x=0$ функция $F(x)$ имеет бесконечный разрыв.
Исследуем далее точку $x=-1$. Поскольку функция $F(x)$ неэлементарная, она может иметь разрыв в этой точке, где меняется ее аналитическое выражение:
$\displaystyle \underset{x \to -1-0}{\textrm{lim}}F(x)=\underset{x \to -1-0}{\textrm{lim}}(2x+5)=3,\; \underset{x \to -1+0}{\textrm{lim}}F(x)=\underset{x \to -1+0}{\textrm{lim}}\frac{1}{x}=-1.$
Найденные односторонние пределы функции конечные, но различные. Поэтому в точке $x=-1$ функция имеет конечный разрыв; ее конечный скачок в этой точке равен
$\displaystyle \underset{x \to -1+0}{\textrm{lim}}F(x)-\underset{x \to -1-0}{\textrm{lim}}F(x)=-4.$
Во всех остальных точках числовой оси функция $F(x)$ непрерывна; ее график показан на рис.3.

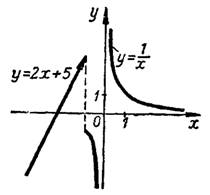
Рис.3