Отыскание функции  по известному ее дифференциалу
по известному ее дифференциалу  [или по известной её производной
[или по известной её производной  ], т. е. действие обратное дифференцированию, называется интегрированием, а искомая функция F(x) называется первообразной функцией от функции
], т. е. действие обратное дифференцированию, называется интегрированием, а искомая функция F(x) называется первообразной функцией от функции  .
.
Всякая непрерывная функция  имеет бесчисленное множество различных первообразных функций, которые отличаются друг от друга постоянным слагаемым: если
имеет бесчисленное множество различных первообразных функций, которые отличаются друг от друга постоянным слагаемым: если  есть первообразная от
есть первообразная от  , т. е. если
, т. е. если  , то и
, то и  , где
, где  — произвольная постоянная, есть также первообразная от
— произвольная постоянная, есть также первообразная от  , поскольку
, поскольку  .
.
Общее выражение  совокупности всех первообразных от функции
совокупности всех первообразных от функции  называется неопределенным интегралом от этой функции и обозначается знаком
называется неопределенным интегралом от этой функции и обозначается знаком  :
:
 если
если 
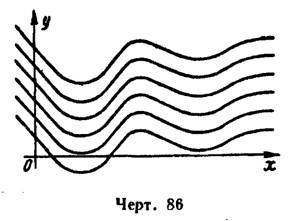
Геометрически, в системе координат  , графики всех первообразных функций от данной функции
, графики всех первообразных функций от данной функции  представляют семейство кривых, зависящее от одного параметра
представляют семейство кривых, зависящее от одного параметра  , которые получаются одна из другой путем параллельного сдвига вдоль оси
, которые получаются одна из другой путем параллельного сдвига вдоль оси  (рис. 86).
(рис. 86).
Свойства неопределенного интеграла.
I. ![\displaystyle \frac{d}{dx}\left [ \int f(x)dx \right ]=f(x)](https://math-helper.net/wp-content/plugins/latex/cache/tex_b6d8ef6961fca502af5ef8676ea12331.gif) или
или 
II.  или
или 
III.  т. е. постоянный множитель можно выносить за знак интеграла.
т. е. постоянный множитель можно выносить за знак интеграла.
IV. ![\displaystyle \int \left [ f_{1}(x)+f_{2}(x)-f_{3}(x) \right ]dx=\int f_{1}(x)dx+\int f_{2}(x)dx-\int f_{3}(x)dx,](https://math-helper.net/wp-content/plugins/latex/cache/tex_4c8ab4ba180eda156952eca4a6b4c49b.gif) т. е. интеграл от суммы равен сумме интегралов от всех слагаемых.
т. е. интеграл от суммы равен сумме интегралов от всех слагаемых.
Основные формулы интегрирования:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
В этих формулах  — постоянная,
— постоянная,  — независимая переменная или любая (дифференцируемая) функция от независимой переменной. Например:
— независимая переменная или любая (дифференцируемая) функция от независимой переменной. Например:
Интеграл  представляет формулу 1 при
представляет формулу 1 при  . Согласно этой формуле,
. Согласно этой формуле,  .
.
Интеграл  представляет формулу 3 при
представляет формулу 3 при  . Согласно этой формуле,
. Согласно этой формуле, 
Интеграл  представляет формулу 8 при
представляет формулу 8 при  . По этой формуле
. По этой формуле  .
.
Интеграл  представляет формулу 11 при
представляет формулу 11 при  . По этой формуле
. По этой формуле  .
.
Интеграл  представляет формулу 2 при
представляет формулу 2 при  , так как
, так как  . По этой формуле
. По этой формуле  . Здесь опущен знак абсолютной величины, ибо всегда
. Здесь опущен знак абсолютной величины, ибо всегда  0" />.
0" />.
Вообще, в формулах 2, 9, 11 следует писать знак абсолютной величины только в тех случаях, когда логарифмируемое выражение может иметь отрицательные значения.
Интеграл  представляет формулу 4 при
представляет формулу 4 при  . Поэтому
. Поэтому  .
.
Интеграл  , так как
, так как  . По формуле 3 при
. По формуле 3 при  получим:
получим:  .
.
Интеграл  , так как
, так как  . По формуле 9 при
. По формуле 9 при  , получим
, получим  .
.
Справедливость формул интегрирования, а также и каждый результат интегрирования можно проверить путем дифференцирования, ибо, как было упомянуто, интегрирование есть действие, обратное дифференцированию.
В простейшем случае, когда заданный интеграл представляет одну из формул интегрирования, задача интегрирования сводится к простому применению этой формулы.
Во всех других случаях задача интегрирования состоит в том, чтобы путем подходящих преобразований привести данный интеграл к одной или нескольким формулам интегрирования, если это возможно.







