Применение определенного интеграла в физике. Практикум по математическому анализу. Урок 92

Пример 11. Прямоугольный резервуар с площадью горизонтального сечения $S=6$ м² наполнен водой до высоты $H=5$ м. Определить время, в течение которого вся вода вытечет из резервуара через небольшое отверстие в его дне площадью $s=0,01$ м², если принять, что скорость истечения воды равна $0,6\sqrt{2gh}$, где $h$ — высота уровня воды над отверстием, $g$ — ускорение силы тяжести.

Решение. Разобьем искомое время $T$ на большое число $n$ малых промежутков $\Delta t_{1},\Delta t_{2},...,\Delta t_{n}$ и пусть за каждый такой промежуток уровень воды в резервуаре понижается на величину $\displaystyle \Delta x=\frac{H}{n}$ (рис. 1).

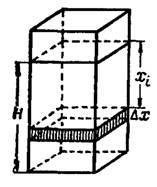
Рис. 1

Если допустить, что в течение каждого малого промежутка времени $\Delta t_{1}$ скорость истечения воды через отверстие в дне остается постоянной, равной ее значению в начале промежутка $0,6\sqrt{2g(H-x_{1})}$, то, приравняв объем воды, вытекшей с такой скоростью через отверстие в дне за промежуток $\Delta t_{1}$ объему опорожнившейся за этот же промежуток части резервуара, получим приближенное равенство

$$0,6s\sqrt{2g(H-x_{i})}\Delta t_{i}\approx S\Delta x,$$

откуда

$$\displaystyle \Delta t_{i}\approx \frac{S\Delta x}{0,6s\sqrt{2g(H-x_{i})}}.$$

Приближенное значение всего искомого времени $T$ будет равно сумме

$$\displaystyle T=\sum_{i=1}^{n}\Delta t_{i}\approx \sum_{i=1}^{n}\frac{S\Delta x}{0,6s\sqrt{2g(H-x_{i})}},\; \; \; \; (*)$$

где по условию задачи точки $x_{i}$ заключены на отрезке $\left [ 0,H \right ]$.

Убедившись, что с возрастанием $n$ погрешность полученного приближенного значения $T$ стремится к нулю, найдем точное значение $T$ как предел интегральной суммы (*) при $n \to +\infty$, т. е. как соответствующий определенный интеграл

$$\displaystyle T=\frac{S}{0,6s\sqrt{2g}}\int_{0}^{H}(H-x)^{-\frac{1}{2}}dx=\frac{S}{0,6s\sqrt{2g}}(H-x)^{\frac{1}{2}} \left.\begin{matrix} \\ \\ \end{matrix}\right| _{H}^{0}=\frac{S}{0,6s}\sqrt{\frac{2H}{g}}.$$

Подставляя числовые значения параметров, получим $T\approx 1010$ сек $\approx 16,83$ мин.

Если бы убыль воды в резервуаре постоянно возмещалась, т. е. если бы уровень воды в нем оставался неизменным, то и скорость истечения воды была бы постоянной, равной $0,6\sqrt{2gH}$. В этом случае в каждую секунду через отверстие в дне резервуара будет вытекать объем воды $0,6\sqrt{2gH}$, равный объему прямого цилиндра с площадью основания $s$ и высотой $0,6\sqrt{2gH}$. Поэтому при указанном предположении объем воды, вмещающейся в резервуаре, вытечет из него за время

$$\displaystyle T_{1}=\frac{SH}{0,6s\sqrt{2gH}}=\frac{1}{2}\frac{S}{0,6s}\sqrt{\frac{2H}{g}}.$$

Сопоставление этого результата с предыдущим показывает, что время истечения $T$, без возмещения убыли воды в резервуаре, в два раза больше времени истечения $T_{1}$, при постоянном возмещении убыли воды; $T=2T_{1}$.

Пример 12. При условиях предыдущей задачи определить, за какое время уровень воды в резервуаре изменится на $h$ м, если сверху в него непрерывно будет протекать $V$ м³ воды в секунду?
Решение. В этом случае за малый промежуток времени $\Delta t$ объем воды в резервуаре изменится на величину

$$S\Delta x\approx \left [ 0,6s\sqrt{2g(H-x)}-V \right ]\Delta t,$$

откуда

$$\displaystyle \Delta t\approx \frac{S\Delta x}{0,6s\sqrt{2g(H-x)-V}}=dt.$$

Интегрируя $dt$ в пределах от $x=0$ до $x=h$, найдем искомое время $T_{2}$, за которое уровень воды в резервуаре изменится на $h$ (м):

$$\displaystyle T_{2}=a\int_{0}^{h}\frac{dx}{\sqrt{H-x}-b},$$

где

$$\displaystyle a=\frac{S}{0,6s\sqrt{2g}},\; b=\frac{V}{0,6s\sqrt{2g}}.$$

Применяя подстановку $\sqrt{H-x}=z$ получим $dx=-2zdz;\: z_{1}=\sqrt{H}$ при $x=0;\: z_{2}=\sqrt{H-h}$ при $x=h$;

$$\displaystyle T_{2}=a\int_{z_{1}}^{z_{2}}\frac{-2zdz}{z-b}=2a\int_{z_{2}}^{z_{1}}\left ( 1+\frac{b}{z-b} \right )dz=2a(z+b\ln \left | z-b \right |) \left.\begin{matrix} \\ \\ \end{matrix}\right| _{\sqrt{H-h}}^{\sqrt{H}}=2a\left ( \sqrt{H}-\sqrt{H-h}+b\ln \left | \frac{\sqrt{H}-b}{\sqrt{H-h}-b} \right | \right ).$$

Здесь изменение уровня воды в резервуаре может быть двояким. Если в начальный момент при $h=0$ скорость притока воды $V$ будет меньше скорости ее убывания из резервуара $0,6s\sqrt{2gH}$, то уровень воды будет понижаться до тех пор, пока эти скорости не станут одинаковыми. После этого вода будет оставаться на постоянном уровне, меньшем первоначального уровня $H$ на величину $h_{1}$ определяемую из уравнения $0,6s\sqrt{2g(H-h_{1})}=V$.
Если же в начале процесса $V>0,6s\sqrt{2gH}$, то уровень воды в резервуаре будет подниматься до тех пор, пока не превысит первоначальный уровень $H$ на величину $h_{2}$, определяемую из уравнения

$$0,6s\sqrt{2g(H+h_{2})}=V,$$

после чего уровень воды в резервуаре будет оставаться неизменным.