Прямолинейные образующие поверхностей второго порядка. Основные формулы
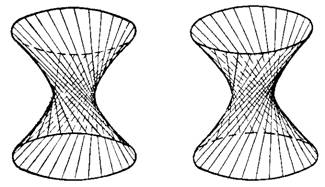
Рис.1 Рис.2
Прямолинейной образующей поверхности называется прямая линия, целиком лежащая на данной поверхности. Например, прямолинейные образующие конической и цилиндрической поверхности.
Однополостный гиперболоид (рис.1,2)

имеет два семейства прямолинейных образующих:

и

где k и l — произвольные параметры, не зависящие от х, у и z.
Каждая из систем (1) и (2) при определенных значениях k и l определяет прямую линию.
При произвольных k и l каждая система дает семейство прямых линий.
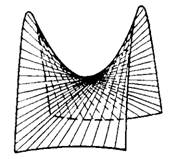
Рис.3
Гиперболический параболоид (рис.3)

имеет также два семейства прямолинейных образующих:

и

где k и l — произвольные параметры.