–Ч–∞–і–∞—З–∞ вДЦ1. –°—В–Њ—А–Њ–љ–∞ —А–Њ–Љ–±–∞ —А–∞–≤–љ–∞ 5 –Є –≤—Л—Б–Њ—В–∞ 4,8. –І–µ—А–µ–Ј –і–≤–µ –њ—А–Њ—В–Є–≤–Њ–ї–µ–ґ–∞—Й–Є–µ –µ–≥–Њ –≤–µ—А—И–Є–љ—Л –њ—А–Њ—Е–Њ–і–Є—В —Н–ї–ї–Є–њ—Б, —Д–Њ–Ї—Г—Б—Л –Ї–Њ—В–Њ—А–Њ–≥–Њ —Б–Њ–≤–њ–∞–і–∞—О—В —Б –і–≤—Г–Љ—П –і—А—Г–≥–Є–Љ–Є –≤–µ—А—И–Є–љ–∞–Љ–Є —А–Њ–Љ–±–∞. –°–Њ—Б—В–∞–≤–Є—В—М —Г—А–∞–≤–љ–µ–љ–Є–µ —Н–ї–ї–Є–њ—Б–∞, –њ—А–Є–љ—П–≤ –і–Є–∞–≥–Њ–љ–∞–ї–Є —А–Њ–Љ–±–∞ –Ј–∞ –Њ—Б–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В.
–†–µ—И–µ–љ–Є–µ. –Ъ–∞–љ–Њ–љ–Є—З–µ—Б–Ї–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ —Н–ї–ї–Є–њ—Б–∞
![]()
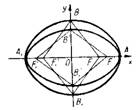
–°–Њ–≥–ї–∞—Б–љ–Њ —Г—Б–ї–Њ–≤–Є—О BF = B'F' = 5, –Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ BOF (—А–Є—Б.1) BF¬≤ = OF¬≤ + OB¬≤,
–љ–Њ OF = c, –Ю–Т = b,
—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, BF = a.
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, b¬≤ + —Б¬≤ = 25. –Э–∞–є–і–µ–Љ –њ–ї–Њ—Й–∞–і—М —А–Њ–Љ–±–∞: S = 5¬Ј4,8 = 24 (–Ї–≤.–µ–і.). –Я–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ BOF —Б–Њ—Б—В–∞–≤–ї—П–µ—В —З–µ—В–≤–µ—А—В—Г—О —З–∞—Б—В—М –њ–ї–Њ—Й–∞–і–Є —А–Њ–Љ–±–∞, —В. –µ. SBOF = 6 –Ї–≤.–µ–і.
–Э–Њ —Б –і—А—Г–≥–Њ–є —Б—В–Њ—А–Њ–љ—Л
![]()
–Њ—В–Ї—Г–і–∞ –ђ—Б= 12.
–†–µ—И–Є–Љ —Б–Є—Б—В–µ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є–є:
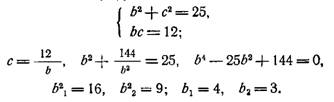
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –Є–Љ–µ–µ–Љ –і–≤–∞ —Н–ї–ї–Є–њ—Б–∞:
![]()
–Ч–∞–і–∞—З–∞ вДЦ2. –Э–∞ —Н–ї–ї–Є–њ—Б–µ x¬≤/36+y¬≤/11=1 –љ–∞–є—В–Є —В–Њ—З–Ї–Є, —А–∞—Б—Б—В–Њ—П–љ–Є—П –Ї–Њ—В–Њ—А—Л—Е –Њ—В –ї–µ–≤–Њ–≥–Њ —Д–Њ–Ї—Г—Б–∞ –±–Њ–ї—М—И–µ —А–∞—Б—Б—В–Њ—П–љ–Є–є –Њ—В –њ—А–∞–≤–Њ–≥–Њ —Д–Њ–Ї—Г—Б–∞ –≤ —В—А–Є —А–∞–Ј–∞.
–†–µ—И–µ–љ–Є—П —Н—В–Є—Е –Ј–∞–і–∞—З –њ–Њ–і—А–Њ–±–љ–Њ –Є–Ј–ї–Њ–ґ–µ–љ–Њ –≤ —Б–ї–µ–і—Г—О—Й–µ–Љ –≤–Є–і–µ–Њ
–Ч–∞–і–∞—З–∞ вДЦ3. –С–Њ–ї—М—И–∞—П –Њ—Б—М —Н–ї–ї–Є–њ—Б–∞ —А–∞–≤–љ–∞ 12, –∞ –і–Є—А–µ–Ї—В—А–Є—Б–∞–Љ–Є —Н—В–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–∞ —Б–ї—Г–ґ–∞—В –њ—А—П–Љ—Л–µ —Е=¬±12. –Э–∞–є—В–Є —Г—А–∞–≤–љ–µ–љ–Є–µ —Н–ї–ї–Є–њ—Б–∞. –І–µ–Љ—Г —А–∞–≤–µ–љ –µ–≥–Њ —Н–Ї—Б—Ж–µ–љ—В—А–Є—Б–Є—В–µ—В?
–†–µ—И–µ–љ–Є–µ. –Ф–ї—П —Б–Њ—Б—В–∞–≤–ї–µ–љ–Є—П —Г—А–∞–≤–љ–µ–љ–Є—П —Н–ї–ї–Є–њ—Б–∞ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Ј–љ–∞—В—М –µ–≥–Њ –њ–Њ–ї—Г–Њ—Б–Є –∞ –Є b. –Я–Њ —Г—Б–ї–Њ–≤–Є—О 2–∞=12, –∞ = 6.
–Я–Њ–ї—Г–Њ—Б—М b –љ–∞—Е–Њ–і–Є–Љ –Є–Ј —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П b¬≤ = –∞¬≤ - —Б¬≤; –∞ —Б –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є, –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–≤ —Г—А–∞–≤–љ–µ–љ–Є—П –і–Є—А–µ–Ї—В—А–Є—Б —Н–ї–ї–Є–њ—Б–∞
—Е = ¬± a¬≤/c.
–Т–Ј—П–≤ –њ—А–∞–≤—Г—О –і–Є—А–µ–Ї—В—А–Є—Б—Г, –њ–Њ–ї—Г—З–Є–Љ
![]()
–Њ—В–Ї—Г–і–∞
![]()
–ђ¬≤ = 36 - 9 = 27, b¬≤ = 27. –Ш–Љ–µ–µ–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ —Н–ї–ї–Є–њ—Б–∞
![]()
–≠–Ї—Б—Ж–µ–љ—В—А–Є—Б–Є—В–µ—В —Н–ї–ї–Є–њ—Б–∞
![]()
–Ю—В–≤–µ—В: ![]()
–Ч–∞–і–∞—З–∞ вДЦ4. –†–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г –і–Є—А–µ–Ї—В—А–Є—Б–∞–Љ–Є —Н–ї–ї–Є–њ—Б–∞ –≤ –і–≤–∞ —А–∞–Ј–∞ –±–Њ–ї—М—И–µ —А–∞—Б—Б—В–Њ—П–љ–Є—П –Љ–µ–ґ–і—Г –µ–≥–Њ —Д–Њ–Ї—Г—Б–∞–Љ–Є. –Ю–њ—А–µ–і–µ–ї–Є—В—М —Н–Ї—Б—Ж–µ–љ—В—А–Є—Б–Є—В–µ—В —Н–ї–ї–Є–њ—Б–∞.
–†–µ—И–µ–љ–Є–µ. –£—А–∞–≤–љ–µ–љ–Є—П –і–Є—А–µ–Ї—В—А–Є—Б —Н–ї–ї–Є–њ—Б–∞ ![]()
–†–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г —Д–Њ–Ї—Г—Б–∞–Љ–Є 2—Б.
–°–Њ–≥–ї–∞—Б–љ–Њ —Г—Б–ї–Њ–≤–Є—О 2—Е = 4—Б, —Е = 2—Б; –љ–Њ ![]()
–Є–Љ–µ–µ–Љ
![]()
–љ–Њ ![]()
–њ–Њ—Н—В–Њ–Љ—Г
![]()
–Ю—В–≤–µ—В: ![]()
–†–µ—И–µ–љ–Є—П —Н—В–Є—Е –Ј–∞–і–∞—З –њ–Њ–і—А–Њ–±–љ–Њ –Є–Ј–ї–Њ–ґ–µ–љ–Њ –≤ —Б–ї–µ–і—Г—О—Й–µ–Љ –≤–Є–і–µ–Њ
–Ч–∞–і–∞—З–∞ вДЦ5. –≠–ї–ї–Є–њ—Б –Ї–∞—Б–∞–µ—В—Б—П –Њ—Б–Є –∞–±—Б—Ж–Є—Б—Б –≤ —В–Њ—З–Ї–µ –Р(4; 0) –Є –Њ—Б–Є –Њ—А–і–Є–љ–∞—В –≤ —В–Њ—З–Ї–µ –Т(0;вАФ3). –°–Њ—Б—В–∞–≤–Є—В—М —Г—А–∞–≤–љ–µ–љ–Є–µ —Н—В–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–∞, –µ—Б–ї–Є –µ–≥–Њ –Њ—Б–Є —Б–Є–Љ–Љ–µ—В—А–Є–Є –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л –Њ—Б—П–Љ –Ї–Њ–Њ—А–і–Є–љ–∞—В (—А–Є—Б.2).
–†–µ—И–µ–љ–Є–µ. –£—А–∞–≤–љ–µ–љ–Є–µ —Н–ї–ї–Є–њ—Б–∞ –±—Г–і–µ—В –Є–Љ–µ—В—М –≤–Є–і
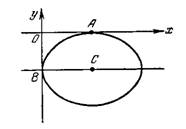
–Ґ–∞–Ї –Ї–∞–Ї —В–Њ—З–Ї–Є –Р –Є –Т —П–≤–ї—П—О—В—Б—П —В–Њ—З–Ї–∞–Љ–Є –Ї–∞—Б–∞–љ–Є—П —Н–ї–ї–Є–њ—Б–∞ –Ї –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ—Л–Љ –Њ—Б—П–Љ, —В–Њ –∞ = 4, b = 3, –∞ —Ж–µ–љ—В—А —Н–ї–ї–Є–њ—Б–∞ –љ–∞—Е–Њ–і–Є—В—Б—П –≤ —В–Њ—З–Ї–µ –°(4;вАФ3).
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —Г—А–∞–≤–љ–µ–љ–Є–µ —Н–ї–ї–Є–њ—Б–∞ –±—Г–і–µ—В:
![]()
–Ю—В–≤–µ—В: ![]()
–Ч–∞–і–∞—З–∞ вДЦ6. –≠–ї–ї–Є–њ—Б –Ї–∞—Б–∞–µ—В—Б—П –Њ—Б–Є –Ю—Г –≤ —В–Њ—З–Ї–µ –Р (0; 5) –Є –њ–µ—А–µ—Б–µ–Ї–∞–µ—В –Њ—Б—М –Ю—Е –≤ —В–Њ—З–Ї–∞—Е –Т(5;0) –Є –°(11;0). –Ч–љ–∞—П, —З—В–Њ –Њ—Б–Є —Н–ї–ї–Є–њ—Б–∞ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ—Л–Љ –Њ—Б—П–Љ, —Б–Њ—Б—В–∞–≤–Є—В—М —Г—А–∞–≤–љ–µ–љ–Є–µ —Н—В–Њ–≥–Њ —Н–ї–ї–Є–њ—Б–∞.







