1. Сложение векторов. Векторы складываются геометрически по правилу параллелограмма или многоугольника.
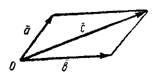
Правило параллелограмма. Суммой двух векторов  и
и  называют такой третий вектор
называют такой третий вектор  , выходящий из их общего начала, который служит диагональю параллелограмма, сторонами которого являются сами векторы (рис.1) и обозначают так:
, выходящий из их общего начала, который служит диагональю параллелограмма, сторонами которого являются сами векторы (рис.1) и обозначают так:  .
.
Правило многоугольника. Чтобы построить сумму любого конечного числа векторов, нужно в конце первого слагаемого вектора построить второй, в конце второго построить третий и т. д. Вектор, замыкающий полученную ломаную линию, представляет собой искомую сумму. Начало его совпадает с началом первого слагаемого вектора, а конец — с концом последнего.
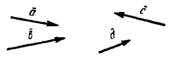
Например, сумма векторов  ,
,  ,
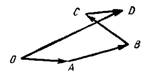
,  и d получается так (рис.2). Строим векторы
и d получается так (рис.2). Строим векторы

Тогда вектор суммы

Два вектора
 и
и  , имеющие равные длины, но противоположные направления, называются противоположными векторами (рис.3).
, имеющие равные длины, но противоположные направления, называются противоположными векторами (рис.3).Если вектор  , противоположен вектору
, противоположен вектору  , то можно записать:
, то можно записать:

Сумма противоположных векторов равна нуль-вектору:

Сумма векторов удостоверяет:
а) закону переместительности:

б) закону сочетательности:

2. Вычитание векторов. Вычитание двух векторов определяется как действие, обратное сложению.
Разностью двух векторов
 и
и  называется такой третий вектор
называется такой третий вектор  , который нужно сложить с вектором
, который нужно сложить с вектором  , чтобы получить вектор
, чтобы получить вектор  , т. е.
, т. е.  , если
, если  .
.Чтобы из вектора
 вычесть вектор
вычесть вектор  , нужно отнести их к общему началу и провести вектор из конечной точки вектора-вычитаемого
, нужно отнести их к общему началу и провести вектор из конечной точки вектора-вычитаемого  конечную точку вектора-уменьшаемого
конечную точку вектора-уменьшаемого  (рис.4).
(рис.4).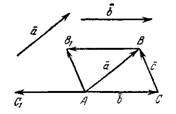

То же действие вычитания двух векторов можно произвести иначе.
Чтобы вычесть из вектора
 вектор
вектор  , надо прибавить к вектору
, надо прибавить к вектору  равный и противоположно направленный вектору
равный и противоположно направленный вектору  вектор (-
вектор (-  ).
).Построим вектор
 , длина которого равна длине вектора
, длина которого равна длине вектора  , а направление его противоположно направлению вектора
, а направление его противоположно направлению вектора  .
.Кроме того, дополним треугольник ABC до параллелограмма АСВВ₁.
Очевидно
 равно
равно  . Следовательно,
. Следовательно,  (рис.4).
(рис.4).Искомая разность

Мы получим следующее равенство:

3. Умножение вектора на скаляр. При умножении вектора
 на скаляр n получим вектор
на скаляр n получим вектор  , коллинеарный с вектором
, коллинеарный с вектором  и имеющий длину в n раз больше, чем
и имеющий длину в n раз больше, чем  . Этот новый вектор
. Этот новый вектор 
имеет одинаковое направление с вектором
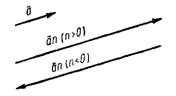
 , если n>0, и противоположное с ним направление, если n<0 (рис.5).
, если n>0, и противоположное с ним направление, если n<0 (рис.5).
Если обозначить одноименной буквой с нуликом вверху  вектор длины, равной 1, и того же направления, что и вектор
вектор длины, равной 1, и того же направления, что и вектор  , то из определения умножения вектора на скаляр следует
, то из определения умножения вектора на скаляр следует

Единичный вектор
 направления вектора
направления вектора  называется его ортом.
называется его ортом.






