Задача № 1. Привести уравнение кривой

к простейшему виду и построить эту кривую. Решение. Группируем члены уравнения, содержащие одноименные координаты:

или

Дополняем члены в скобках до полных квадратов:

или

Обозначаем  . Произведенная замена представляет собой параллельное пересечение осей координат. Сравнивая последние соотношения с формулами
. Произведенная замена представляет собой параллельное пересечение осей координат. Сравнивая последние соотношения с формулами

находим координаты нового начала:  т. е. новое начало координат O₁ помещается в точке (3; —1).
т. е. новое начало координат O₁ помещается в точке (3; —1).
Уравнение (а) в новой системе осей координат принимает вид:

Делим обе части этого уравнения на 45, получаем каноническое уравнение данной кривой

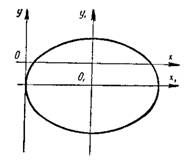
Таким образом, заданное уравнение определяет эллипс с полуосями  и центром, находящимся в первоначальной системе координат, в точке O₁(3; -1) (рис.1).
и центром, находящимся в первоначальной системе координат, в точке O₁(3; -1) (рис.1).
Задача № 2. Упростить уравнение кривой

и схематически построить эту кривую. Решение. Группируем члены с одноименными ко¬ординатами:  или
или  . Дополняем член в скобках до полного квадрата
. Дополняем член в скобках до полного квадрата

или

Обозначаем:  Сравнивая последние соотношения с формулами
Сравнивая последние соотношения с формулами

находим координаты нового начала:  т. е. новое начало координат помещается в точке O₁(-1;-3).
т. е. новое начало координат помещается в точке O₁(-1;-3). 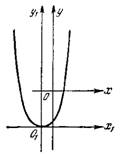
Уравнение (а) в новой системе координат принимает вид:

или

Заданное уравнение определяет параболу с вершиной в точке O₁(-1; -3), осью симметрии  , параллельной оси ординат и параметром
, параллельной оси ординат и параметром  (рис. 2).
(рис. 2).