Векторным произведением вектора  на вектор
на вектор  называется новый вектор
называется новый вектор  , длина которого численно равна площади параллелограмма, построенного на векторах
, длина которого численно равна площади параллелограмма, построенного на векторах  и
и  , перпендикулярный к плоскости этих векторов и направленный в такую сторону, чтобы кратчайший поворот от
, перпендикулярный к плоскости этих векторов и направленный в такую сторону, чтобы кратчайший поворот от  к
к  вокруг полученного вектора
вокруг полученного вектора  представлялся происходящим против часовой стрелки, для правой системы координат, если смотреть с конца вектора
представлялся происходящим против часовой стрелки, для правой системы координат, если смотреть с конца вектора  .
.
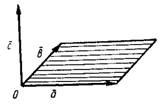
Рис.1
Векторное произведение обозначается символом
 или
или ![\vec{c}=\left[\vec{a} \vec{b}\right].](https://math-helper.net/wp-content/plugins/latex/cache/tex_869a8857f21261d649f50829d23e8eee.gif)
Из определения следует, что длина вектора  равна:
равна:

т. е. произведению длин перемножаемых векторов, умноженному на синус угла между ними, где φ — угол между векторами
 и
и  .
.Векторное произведение ненулевых векторов равно нулю тогда и только тогда, когда векторы
 и
и  коллинеарны (параллельны).
коллинеарны (параллельны).Таким образом, условие коллинеарности векторов:
![\left[\vec{a\vec{b}} \right]=0.\; \; \; \left(2 \right)](https://math-helper.net/wp-content/plugins/latex/cache/tex_f2ddfc91014733f9e53fbb0d9cb2943b.gif)
В частности,
![\left[\vec{a\vec{a}} \right]=0.\; \; \; \left(3 \right)](https://math-helper.net/wp-content/plugins/latex/cache/tex_6d845b0636ecf3641341ccdaa436e7e2.gif)
Основные свойства векторного произведения:
1. При перестановке сомножителей векторное произведение меняет знак:

2. Векторное произведение обладает свойством сочетательности относительно числового множителя:
![\lambda \left[\vec{a}\vec{b} \right]=\left[\lambda \vec{a}\: \vec{b} \right]=\left[\vec{a}\: \lambda \vec{b} \right],\; \; \; \left(5 \right)](https://math-helper.net/wp-content/plugins/latex/cache/tex_db7219819aa41384fa96b6c14a64ce72.gif)
т. е. чтобы умножить векторное произведение на число, достаточно умножить на это число один из сомножителей.
3. Векторное произведение подчиняется распределительному свойству:
![\left[\left(\vec{a}+\vec{b} \right) \vec{c}\right]=\left[\vec{a}\vec{c} \right]+\left[\vec{b}\vec{c} \right].\; \; \; \left(6 \right)](https://math-helper.net/wp-content/plugins/latex/cache/tex_5f3e467359e922a355430c84e91c5954.gif)
Если векторы
 и
и  заданы своими проекциями
заданы своими проекциями
то
![\left[\vec{a}\vec{b} \right]=\left(y_{1}z_{2}-y_{2}z_{1} \right)\vec{i}+\left(z_{1}x_{2}-z_{2}x_{1} \right)\vec{j}+\left(x_{1}y_{2}-x_{2}y_{1}\right)\vec{k},\; \; \; \left(7 \right)](https://math-helper.net/wp-content/plugins/latex/cache/tex_ec01655067ae167b6e0c213f665308a7.gif)
или
![\left[\vec{a}\vec{b} \right]=\begin{vmatrix} y_{1} & z_{1}\\ y_{2} & z_{2} \end{vmatrix}\vec{i}-\begin{vmatrix} x_{1}&z_{1} \\ x_{2} & z_{2} \end{vmatrix}\vec{j}+\begin{vmatrix} x_{1} &y_{1} \\ x_{2} & y_{2} \end{vmatrix}\vec{k}.\; \; \; \left(8 \right)](https://math-helper.net/wp-content/plugins/latex/cache/tex_9ac6a90e3a9ed3f9d0da0b8bc9bd347e.gif)
Эти три определителя получаются из таблицы (матрицы) проекций данных векторов

вычеркиванием по очереди 1-го, 2-го и 3-го столбцов.
Векторное произведение может быть записано в символической форме с помощью определителя третьего порядка:
![\left[\vec{a}\vec{b} \right]=\begin{vmatrix} \vec{i} &\vec{j} &\vec{k} \\ x_{1} & y_{1} &z_{1} \\ x_{2}&y_{2} & z_{2} \end{vmatrix}.\; \; \; \left(9 \right)](https://math-helper.net/wp-content/plugins/latex/cache/tex_250768448616c87d4eaf3007568cfada.gif)
Условия коллинеарности (параллельности) двух векторов заданных проекциями, получаются из равенства (3):

Площадь треугольника, построенного на двух заданных векторах, исходящих из одной точки, выражается
![S=\frac{1}{2}\left|\left[\vec{a}\vec{b} \right] \right|=\frac{1}{2}\sqrt{\begin{vmatrix} y_{1} &z_{1} \\ y_{2} & z_{2} \end{vmatrix}^{2}+\begin{vmatrix} x_{1} &z_{1} \\ x_{2} & z_{2} \end{vmatrix}^{2}+\begin{vmatrix} x_{1} &y_{1} \\ x_{2}& y_{2} \end{vmatrix}^{2}}\; \; \left(11 \right)](https://math-helper.net/wp-content/plugins/latex/cache/tex_5ba35271bd8a6023b7571fea73ced62e.gif)
Угол между двумя векторами находится по формуле:
![\sin \phi =\frac{\left|\left[\vec{a}\vec{b} \right] \right|}{ab}=\frac{\sqrt{\begin{vmatrix} y_{1} &z_{1} \\ y_{2} & z_{2} \end{vmatrix}^{2}+\begin{vmatrix} x_{1} &z_{1} \\ x_{2} & z_{2} \end{vmatrix}^{2}+\begin{vmatrix} x_{1} &y_{1} \\ x_{2}& y_{2} \end{vmatrix}^{2}}}{\sqrt{x_{1}^{2}+y_{1}^{2}+z_{1}^{2} }\cdot\sqrt{x_{2}^{2}+y_{2}^{2}+z_{2}^{2}}}.\; \; \left(12 \right)](https://math-helper.net/wp-content/plugins/latex/cache/tex_d3e339b4bfab4458e8c10be54f122b5d.gif)







