–†–∞–і–Є–∞–љ–љ–Њ–µ –Є–Ј–Љ–µ—А–µ–љ–Є–µ —Г–≥–ї–Њ–≤. –£—З–Є–Љ—Б—П —А–µ—И–∞—В—М –Ј–∞–і–∞—З–Є –њ–Њ —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є–Є. –Т–Є–і–µ–Њ—Г—А–Њ–Ї вДЦ1
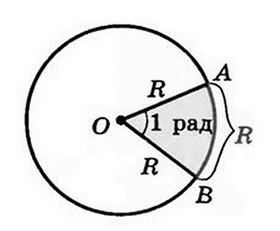
–Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ. –£–≥–ї–Њ–Љ –≤ 1 —А–∞–і–Є–∞–љ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —Ж–µ–љ—В—А–∞–ї—М–љ—Л–є —Г–≥–Њ–ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Ї–Њ—В–Њ—А—Л–є –Њ–њ–Є—А–∞–µ—В—Б—П –љ–∞ –і—Г–≥—Г, –і–ї–Є–љ–∞ –Ї–Њ—В–Њ—А–Њ–є —А–∞–≤–љ–∞ —А–∞–і–Є—Г—Б—Г –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є.
–†–∞–і–Є–∞–љ–љ–∞—П –Љ–µ—А–∞ —Г–≥–ї–∞ –љ–µ –Ј–∞–≤–Є—Б–Є—В –Њ—В —А–∞–і–Є—Г—Б–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –Є–Ј –Ї—Г—А—Б–∞ –≥–µ–Њ–Љ–µ—В—А–Є–Є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –і–ї–Є–љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–љ–∞  , —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –і–ї–Є–љ–∞ –њ–Њ–ї—Г–Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–љ–∞
, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –і–ї–Є–љ–∞ –њ–Њ–ї—Г–Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–љ–∞  . –Ч–љ–∞—З–Є—В —А–∞–і–Є–∞–љ–љ–∞—П –Љ–µ—А–∞ –њ–Њ–ї—Г–Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–љ–∞
. –Ч–љ–∞—З–Є—В —А–∞–і–Є–∞–љ–љ–∞—П –Љ–µ—А–∞ –њ–Њ–ї—Г–Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–љ–∞  , –∞ –µ—С –≥—А–∞–і—Г—Б–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞ —А–∞–≤–љ–∞
, –∞ –µ—С –≥—А–∞–і—Г—Б–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞ —А–∞–≤–љ–∞  . –≠—В–Њ –њ–Њ–Ј–≤–Њ–ї—П–µ—В —Г—Б—В–∞–љ–Њ–≤–Є—В—М —Б–≤—П–Ј—М –Љ–µ–ґ–і—Г —А–∞–і–Є–∞–љ–љ–Њ–є –Є –≥—А–∞–і—Г—Б–љ–Њ–є –Љ–µ—А–∞–Љ–Є —Г–≥–ї–∞.
. –≠—В–Њ –њ–Њ–Ј–≤–Њ–ї—П–µ—В —Г—Б—В–∞–љ–Њ–≤–Є—В—М —Б–≤—П–Ј—М –Љ–µ–ґ–і—Г —А–∞–і–Є–∞–љ–љ–Њ–є –Є –≥—А–∞–і—Г—Б–љ–Њ–є –Љ–µ—А–∞–Љ–Є —Г–≥–ї–∞.
 —А–∞–і=
—А–∞–і= , –Њ—В—Б—О–і–∞ 1 —А–∞–і=
, –Њ—В—Б—О–і–∞ 1 —А–∞–і= . –†–∞–Ј–і–µ–ї–Є–Љ 180 –љ–∞ 3,14, –њ–Њ–ї—Г—З–Є–Љ, —З—В–Њ 1 —А–∞–і
. –†–∞–Ј–і–µ–ї–Є–Љ 180 –љ–∞ 3,14, –њ–Њ–ї—Г—З–Є–Љ, —З—В–Њ 1 —А–∞–і  . –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г
. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г  —А–∞–і=
—А–∞–і= , –Ј–љ–∞—З–Є—В
, –Ј–љ–∞—З–Є—В  —А–∞–і...
—А–∞–і...
–Я–Њ–ї–љ—Л–є —Г—А–Њ–Ї —Б–Љ–Њ—В—А–Є—В–µ –≤ —Б–ї–µ–і—Г—О—Й–µ–Љ –≤–Є–і–µ–Њ:
–Ф–Њ–Љ–∞—И–љ–µ–µ –Ј–∞–і–∞–љ–Є–µ:
1. –Э–∞–є—В–Є —А–∞–і–Є–∞–љ–љ—Г—О –Љ–µ—А—Г —Г–≥–ї–Њ–≤, –Ј–∞–і–∞–љ–љ—Л—Е –≤ –≥—А–∞–і—Г—Б–∞—Е:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  .
.
2. –Ч–∞–њ–Є—Б–∞—В—М –≥—А–∞–і—Г—Б–љ—Г—О –Љ–µ—А—Г —Г–≥–ї–Њ–≤, –Ј–∞–і–∞–љ–љ—Л—Е –≤ —А–∞–і–Є–∞–љ–∞—Е:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  .
.
3. –°—А–∞–≤–љ–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Л —Г–≥–ї–Њ–≤, –Ј–∞–і–∞–љ–љ—Л—Е –≤ —А–∞–і–Є–∞–љ–∞—Е:
1)  –Є 1;
–Є 1;
2)  –Є
–Є  .
.
4. –Ю—В–Љ–µ—В—М—В–µ –љ–∞ –µ–і–Є–љ–Є—З–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —В–Њ—З–Ї—Г, –њ–Њ–ї—Г—З–µ–љ–љ—Г—О –њ—А–Є –њ–Њ–≤–Њ—А–Њ—В–µ —В–Њ—З–Ї–Є  –љ–∞ —Г–≥–Њ–ї:
–љ–∞ —Г–≥–Њ–ї:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  .
.
5. –Т –Ї–∞–Ї–Њ–є —З–µ—В–≤–µ—А—В–Є –љ–∞—Е–Њ–і–Є—В—Б—П —В–Њ—З–Ї–∞ –µ–і–Є–љ–Є—З–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –њ–Њ–ї—Г—З–µ–љ–љ–∞—П –њ—А–Є –њ–Њ–≤–Њ—А–Њ—В–µ —В–Њ—З–Ї–Є  –љ–∞ —Г–≥–Њ–ї:
–љ–∞ —Г–≥–Њ–ї:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  ; 11)
; 11)  ; 12)
; 12)  ; 13) 1; 14) -3.
; 13) 1; 14) -3.
6. –Ъ–∞–Ї–Є–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –Є–Љ–µ–µ—В —В–Њ—З–Ї–∞ –µ–і–Є–љ–Є—З–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –њ–Њ–ї—Г—З–µ–љ–љ–∞—П –њ—А–Є –њ–Њ–≤–Њ—А–Њ—В–µ —В–Њ—З–Ї–Є  –љ–∞ —Г–≥–Њ–ї:
–љ–∞ —Г–≥–Њ–ї:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  .
.







