Исследовать функцию и построить график (решение примера). Практикум по математическому анализу. Урок 60

Пример 2. Исследовать функцию $\displaystyle y=\frac{1-x^{3}}{x^{2}}$ и построить ее график.
Решение. I. Функция $\displaystyle y=\frac{1-x^{3}}{x^{2}}$ определена на всей числовой оси, кроме точки x=0.
II. В точке $x=0$ функция имеет бесконечный разрыв: при $x \to -\infty$ и при $x \to +0 ,\: \lim y=+\infty$. Во всех других точках числовой оси функция непрерывна.
III. Функция не является ни четной, ни нечетной, ни периодической.
IV. График функции пересекает ось Ох в точке (1; 0) и не пересекает оси Оу.
Слева от точки разрыва, при $-\infty<x<0,\: y>0$; между точкой разрыва и точкой пересечения с осью Ох, при $0 <x<1,\: y>0$; справа от точки пересечения с осью Ох, при 1<x< $+\infty<y< 0$.
V. а) Прямая х = 0 (ось ординат) является вертикальной асимптотой графика функции, ибо при х = 0 она имеет бесконечный разрыв;
б) $\displaystyle k=\underset{x \to +\infty }{\lim }\frac{y}{x}=\underset{x \to +\infty }{\lim }\frac{1-x^{3}}{x^{3}}=-1$;
$\displaystyle b=\underset{x \to +\infty }{\lim }(y-kx)=\underset{x \to +\infty }{\lim }\left ( \frac{1-x^{3}}{x^{3}}+x \right )=\underset{x \to +\infty }{\lim }\frac{1}{x^{2}}=0$.
Следовательно, прямая y=-x есть невертикальная асимптота. При $\displaystyle x \to -\infty$ параметры k и b имеют те же значения, поэтому других асимптот нет.
VI. $\displaystyle y'=-\frac{x^{3}+2}{x^{3}};\: y'=0$ в точке $\displaystyle x=-\sqrt[3]{2}$, которая является критической; у' не существует в точке х = 0, но эта точка не является критической, так как она есть точка разрыва.
Исследуем критическую точку по знаку y'':

$\displaystyle y''=\frac{6}{x^{4}};\: y''(-\sqrt[3]{2}>0)$,

следовательно, $x=-\sqrt[3]{2}$ есть точка минимума:

$\displaystyle y_{min}=y(-\sqrt[3]{2})=\frac{3}{\sqrt[3]{4}}.$

Слева от точки минимума при $x \in (-\infty;-\sqrt[3]{2})$, $y'<0$ функция убывает; между точкой минимума и точкой разрыва при $x\in (-\sqrt[3]{2};0;),\, y'>0$ функция возрастает; справа от точки разрыва при $x\in (0;+\infty;)$, y'<0 функция убывает.

VII. $\displaystyle y''=\frac{6}{x^{4}};\: y''\neq 0$; y'' не существует при х = 0, но это значение х не может быть абсциссой точки перегиба, так как оно является точкой разрыва. Следовательно, график функции не имеет точек перегиба.
Во всей области определения функции $y''>0$, поэтому ее график всюду обращен выпуклостью вниз.
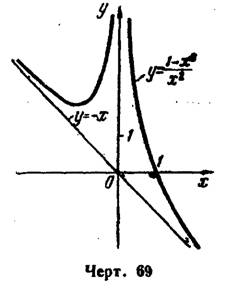
VIII. Используя все полученные данные, строим график функции (рис. 69).
Пример 3. Исследовать функцию $\displaystyle y=\sqrt[3]{(x+1)^{2}-\sqrt[3]{(x-1)^{2}}}$ и построить ее график.
Решение. I, II. Функция $\displaystyle y=\sqrt[3]{(x+1)^{2}}-\sqrt[3]{(x-1)^{2}}$ определена и непрерывна на всей числовой оси.
III. Функция нечетная, ибо у(-х)=-у(х); ее график будет симметричен относительно начала координат.
IV. График функции пересекается с осями координат только в начале координат.
При х<0 значения у<0; при х>0 значения y>0.
V. а) Вертикальных асимптот график функции не имеет;
б) $\displaystyle k=\underset{x \to +\infty }{\lim}\frac{y}{x}=\underset{x \to +\infty }{\lim}\frac{\sqrt[3]{(x+1)^{2}}-\sqrt[3]{(x-1)^{2}}}{x}=\underset{x \to +\infty }{\lim}\left ( \sqrt[3]{\frac{1}{x}+\frac{2}{x^{2}}+\frac{1}{x^{3}}}-\sqrt[3]{\frac{1}{x}-\frac{2}{x^{2}}+\frac{1}{x^{3}}} \right )=0;$
$\displaystyle b=\underset{x \to +\infty }{\lim}(y-kx)=\underset{x \to +\infty }{\lim}\left [ \sqrt[3]{(x+1)^{2}}-\sqrt[3]{(x-1)^{2}} \right ]=\underset{x \to +\infty }{\lim}\frac{(x+1)^{2}-(x-1)^{2}}{\sqrt[3]{(x+1)^{4}}+\sqrt[3]{(x+1)^{2}(x-1)^{2}}+\sqrt[3]{(x-1)^{4}}}=0.$
Подставляя найденные значения k=b=0 в уравнение y=kx+b получим уравнение невертикальной асимптоты: y=0.
Тот же результат получится и при $x \to -\infty$.
VI. $\displaystyle y'=\frac{2}{3}(x+1)^{-\frac{1}{3}}-\frac{2}{3}(x-1)^{-\frac{1}{3}}=\frac{2}{3}\cdot \frac{\sqrt[3]{x-1}-\sqrt[3]{x+1}}{\sqrt[3]{x^{2}-1}};$
у' нигде не обращается в нуль; у' не существует в точках $x=\pm 1$, которые являются критическими. Исследуя критические точки по знаку у' в соседних с ними точках слева и справа:

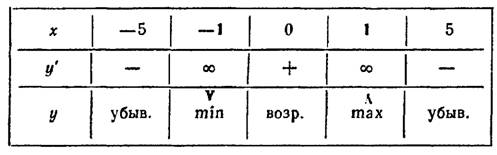
заключаем, что x=-1 есть точка минимума, где $y_{min}=y(-1)=-\sqrt[3]{4}$ а х=1 есть точка максимума, где $y_{max}=y(1)=\sqrt[3]{4}$.
Слева от точки минимума в интервале $(-\infty ;-1)$ и справа от точки максимума в интервале $(1;+\infty)$, где у'<0, функция убывает, а между точками минимума и максимума в интервале (—1; 1), где y'>0, функция возрастает.
VII. $\displaystyle y''=-\frac{2}{9}(x+1)^{-\frac{4}{3}}+\frac{2}{9}(x-1)^{-\frac{4}{3}}=\frac{2}{9}\cdot \frac{\sqrt[3]{(x+1)^{4}}-\sqrt[3]{(x-1)^{4}}}{\sqrt[3]{(x^{2}-1)^{4}}};$
y''=0 в точке х=0; у" не существует в точках х = ±1. Эти точки оси Ох могут быть абсциссами точек перегиба. Исследуя их по знаку у" в соседних с ними точках слева и справа:

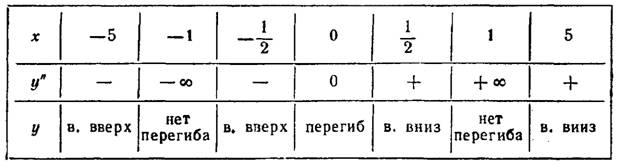
заключаем, что х=0 есть абсцисса точки перегиба; у(0) = 0.

Слева от точки перегиба, в интервале $(-\infty ;0)$, где у"<0, график функции обращен выпуклостью вверх, а справа от точки перегиба, в интервале $(0:+\infty)$, где у">0, график функции обращен выпуклостью вниз.
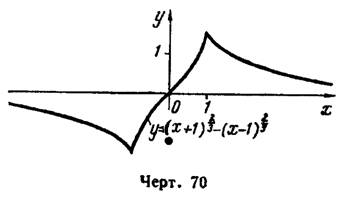
VIII. Основываясь на полученных результатах исследования, строим график функции (рис. 70).