Максимум и минимум (экстремум) функции. Практикум по математическому анализу. Урок 52

Значение функции $f(x)$ в точке $x_{0}$ называется максимумом (минимумом), если оно является наибольшим (наименьшим) по сравнению с ее значениями во всех достаточно близких точках слева и справа от $x_{0}$.
Функция может иметь экстремум (максимум или минимум) только в тех точках, которые лежат внутри области определения функции и где ее производная равна нулю или не существует. (Это необходимые условия экстремума, но недостаточные; они могут выполняться и в точках, где нет экстремума, например в точках $x_{2},x_{5},x_{7}$ рис. 44.) Такие точки называются критическими. В соответствующих точках графика функции касательная параллельна оси абсцисс ($y'=0$), или оси ординат ($y'=\infty$) или нет определенной касательной (например, как в угловой точке).

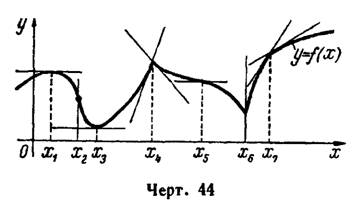
На графике функции (рис. 44) отчетливо видно, что точками экстремума являются все точки, где функция меняет свое направление и непрерывна.
Точки $x_{1}$ и $x_{4}$, при переходе через которые аргумента $x$ возрастание функции сменяется на убывание, являются точками максимума, а точки $x_{3}$ и при переходе через которые аргумента $x$ убывание функции сменяется на возрастание, являются точками минимума.
Поскольку поведение функции характеризуется знаком ее производной, то функция будет иметь экстремум в тех точках, где ее производная меняет свой знак, а сама функция непрерывна. Это достаточные условия экстремума (если они выполнены в какой-либо точке, то она обязательно будет точкой экстремума).
Отсюда вытекает следующее правило исследования функции на экстремум.
Чтобы найти точки экстремума функции $y=f(x)$, в которых она непрерывна, нужно:
I. Найти производную $y'$ и критические точки, в которых $y'=0$ или не существует, а сама функция непрерывна, и которые лежат внутри области определения функции.
IIа. Определить знак $y'$ слева и справа от каждой критической точки.
Если при переходе аргумента $x$ через критическую точку $x_{0}$:
1) $y'$ меняет знак с + на —, то $x_{0}$ есть точка максимума;
2) $y'$ меняет знак с — на +, то $x_{0}$ есть точка минимума;
3) $y'$ не меняет знака, то в точке $x_{0}$ нет экстремума.
Иногда проще исследовать критические точки, где $y'=0$, по знаку второй производной,— вместо правила IIа можно пользоваться следующим правилом:
IIб. Найти вторую производную $y''$ и определить ее знак в каждой критической точке.
Если в критической точке $x_{0}$, где $y'=0$:
1) $y''>0$, то $x_{0}$ есть точка минимума;
2) $y''<0$, то $x_{0}$ есть точка максимума;
3) $y''=0$, то вопрос о наличии экстремума в точке $x_{0}$ остается открытым. Такую критическую точку, как и всякую другую, можно исследовать по правилу IIа.
Далее следует найти экстремумы функции, т. е. вычислить значения функции в найденных точках экстремума.
При исследовании на экстремум некоторых типов функций возможны существенные упрощения. Например, если функция представляет дробь с постоянным числителем или корень с целым положительным показателем.
Характер упрощений, возможных при исследовании на экстремум указанных функций, разъясняется в решении задачи №2.