Примеры. Исследовать на максимум и минимум функции:
1)  ; 2)
; 2)  ; 3)
; 3) ![v=2\sqrt[3]{x^{5}}-5\sqrt[3]{x^{2}}+1](https://math-helper.net/wp-content/plugins/latex/cache/tex_fe7815f37443c4ff60eacf2d5684b06c.gif) ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  .
.
Решение. 1) Согласно правилу исследования функции на экстремум:
I. Находим производную:  и критические точки. Полагая
и критические точки. Полагая  , получим
, получим  . Функция
. Функция  определена и непрерывна на всей числовой оси. Поэтому точки
определена и непрерывна на всей числовой оси. Поэтому точки  и
и  являются критическими.
являются критическими.
Других критических точек нет, так как производная  существует всюду.
существует всюду.
II. Исследуем критические точки, определяя знак  слева и справа от каждой этой точки (по правилу IIа). Для сокращения вычислений и для наглядности это исследование удобно записать в виде следующей таблицы:
слева и справа от каждой этой точки (по правилу IIа). Для сокращения вычислений и для наглядности это исследование удобно записать в виде следующей таблицы:
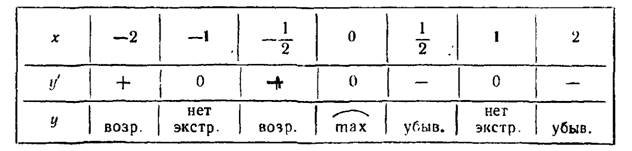
В первой строке помещены все критические точки в порядке расположения их на числовой оси; между ними вставлены промежуточные точки, расположенные слева и справа от критических точек. Во второй строке помещены знаки производной в указанных промежуточных точках, т. е. знаки  и
и  .
.
В третьей строке — заключение о поведении функции. Исследуемая функция имеет одну точку экстремума — точку максимума  , где
, где  . До этой точки в интервале
. До этой точки в интервале  функция неизменно возрастает, а после нее в интервале
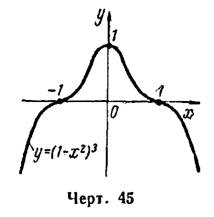
функция неизменно возрастает, а после нее в интервале  она неизменно убывает (рис. 45).
она неизменно убывает (рис. 45).
2) I. Ищем критические точки. Производная  обращается в нуль при
обращается в нуль при  и не существует (разрывна) при
и не существует (разрывна) при  . Однако критическими точками являются только точки
. Однако критическими точками являются только точки  и
и  : они лежат внутри области определения функции
: они лежат внутри области определения функции  , которая представляет отрезок [ — 1; 1], и в них эта функция непрерывна. Точки
, которая представляет отрезок [ — 1; 1], и в них эта функция непрерывна. Точки  и
и  не являются критическими, так как они лежат не внутри области определения функции
не являются критическими, так как они лежат не внутри области определения функции  , а на ее границах.
, а на ее границах.
II. Исследуем критические точки по знаку производной  в соседних с ними точках. Составим следующую таблицу:
в соседних с ними точках. Составим следующую таблицу:
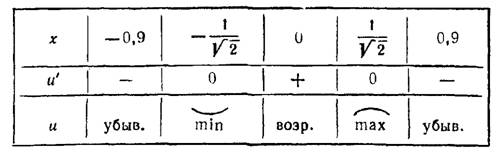
Согласно этой таблице функция и имеет две точки экстремума: точку минимума  , где
, где  и точку максимума
и точку максимума  ,где
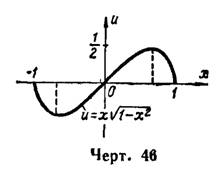
,где  (рис. 46).
(рис. 46).
3) I. Находим производную
![\displaystyle v'=2\cdot \frac{5}{3}x^{\frac{2}{3}}-5\cdot \frac{2}{3}x^{-\frac{1}{3}}=\frac{10}{3}\cdot \frac{x-1}{\sqrt[3]{x}}](https://math-helper.net/wp-content/plugins/latex/cache/tex_1cd722ca37cf5d5413cf8dcfe717ff8e.gif)
и критические точки:
 при
при  ;
;  не существует (равна
не существует (равна  ) при
) при  . Функция
. Функция  определена и непрерывна на всей числовой оси. Поэтому обе найденные точки являются критическими.
определена и непрерывна на всей числовой оси. Поэтому обе найденные точки являются критическими.II. Исследуем критические точки по знаку производной
 в соседних с ними точках. Составим таблицу:
в соседних с ними точках. Составим таблицу: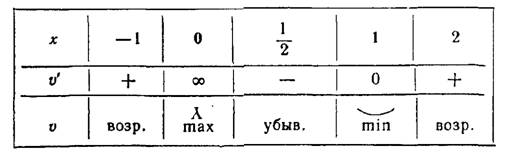
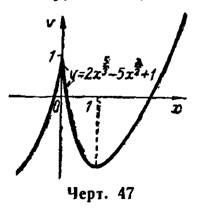
Из таблицы следует, что функция
 имеет две точки экстремума: точку максимума
имеет две точки экстремума: точку максимума  , где
, где  , и точку минимума
, и точку минимума  , где
, где  (рис. 47).
(рис. 47).4) I. Найдем критические точки. Производная
 равна нулю в точках
равна нулю в точках  . Эти точки являются критическими, так как функция
. Эти точки являются критическими, так как функция  определена и непрерывна на всей числовой оси. Производная
определена и непрерывна на всей числовой оси. Производная  существует всюду. Поэтому других критических точек функция
существует всюду. Поэтому других критических точек функция  не имеет.
не имеет.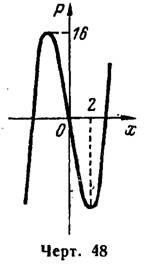
II. Исследуем критические точки по знаку второй производной
 в самих этих точках (по правилу II б):
в самих этих точках (по правилу II б):  , следовательно, критическая точка
, следовательно, критическая точка  есть точка максимума, где
есть точка максимума, где  0" />, поэтому критическая точка
0" />, поэтому критическая точка  есть точка минимума, где
есть точка минимума, где  (рис. 48).
(рис. 48).5) I. Ищем производную
 и критические точки:
и критические точки:  обращается в нуль в точке
обращается в нуль в точке  . В этой точке функция
. В этой точке функция  непрерывна, но она не лежит внутри области определения функции
непрерывна, но она не лежит внутри области определения функции  , которая представляет интервал
, которая представляет интервал  .
. 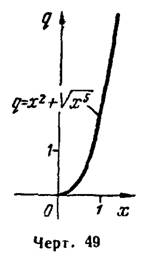
Поэтому точка
 не является критической;
не является критической;  не обращается в нуль в других точках и существует во всей области определения функции. Поэтому функция
не обращается в нуль в других точках и существует во всей области определения функции. Поэтому функция  , как не имеющая ни одной критической точки, не имеет экстремума. Во всей своей области определения она неизменно (монотонно) возрастает, ибо
, как не имеющая ни одной критической точки, не имеет экстремума. Во всей своей области определения она неизменно (монотонно) возрастает, ибо  во всей этой области (рис. 49).
во всей этой области (рис. 49).Если не учесть, что точка
 не лежит внутри области определения функции
не лежит внутри области определения функции  , то, применяя правило IIб,
, то, применяя правило IIб,  0" />, приходим к ошибочному заключению, что в этой точке функция
0" />, приходим к ошибочному заключению, что в этой точке функция  имеет минимум.
имеет минимум.6) I. Находим критические точки:
 при
при  .
.Все точки
 являются критическими, так как функция
являются критическими, так как функция  определена и непрерывна на всей числовой оси;
определена и непрерывна на всей числовой оси;  существует всюду, поэтому других критических точек нет.
существует всюду, поэтому других критических точек нет.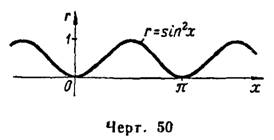
II. Исследуем критические точки по знаку второй производной в самих этих точках:
 . При четном
. При четном  ,
,  0" />, точки
0" />, точки  являются точками минимума, где
являются точками минимума, где  ; при нечетном
; при нечетном  ,
,  , точки
, точки  являются точками максимума, где
являются точками максимума, где  (рис. 50).
Здесь оказалось, что у функции
(рис. 50).
Здесь оказалось, что у функции  максимумы и минимумы строго чередуются. То же будет и у любой непрерывной функции, имеющей несколько экстремумов.
максимумы и минимумы строго чередуются. То же будет и у любой непрерывной функции, имеющей несколько экстремумов.






