Определители третьего порядка

Выражение вида

называется определителем третьего порядка.
Определитель третьего порядка имеет девять элементов, три строки, три столбца, две диагонали — главную и побочную.

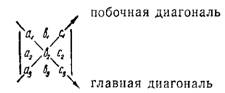
Формула (1) показывает, что в раскрытом виде определитель содержит шесть членов. Для их определения существуют простые способы. Рассмотрим два из них.
Способ I. Выписываем все элементы определителя в том же порядке, как они расположены в определителе, и приписываем справа первые два столбца определителя:

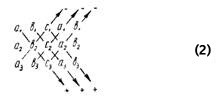
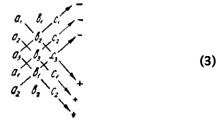
Способ II. Возьмем со знаком плюс произведение элементов, стоящих на главной диагонали определителя, а также произведения элементов, стоящих на двух параллельных к ней линиях, содержащих по три элемента.
Произведения же элементов, стоящих на побочной диагонали и на двух параллельных к ней линиях, содержащих по три элемента, возьмем со знаком минус.
Алгебраическая сумма этих шести произведений дает значение определителя третьего порядка.



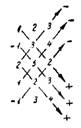
Пример. Вычислить определитель:


$\begin{vmatrix} 1 & 2 &3 \\ -1 &3 &4 \\ 2& 5 & 2 \end{vmatrix}$


Решение.


$\begin{vmatrix} 1 & 2 &3 \\ -1 &3 &4 \\ 2& 5 & 2 \end{vmatrix}=1\cdot 3\cdot 2+(-1)\cdot 5\cdot 3+2\cdot 2\cdot 4-2\cdot 3\cdot 3-1\cdot 5\cdot 4-(-1)\cdot 2\cdot 2=-27.$

Способ III. Способ разложения определителя по элементам какой-либо строки или столбца.
Если в определителе третьего порядка вычеркнуть одну строку и один столбец, на пересечении которых стоит некоторый элемент, то оставшиеся элементы образуют определитель второго порядка, который называется минором определителя Δ, соответствующим этому элементу. Например, минором определителя

$$\Delta=\begin{vmatrix} a_{1} &b_{1} & c_{1}\\ a_{2} &b_{2} & c_{2} \\ a_{3} &b_{3} & c_{3} \end{vmatrix},$$

соответствующим элементу $\; b_{3}\;$ будет определитель второго порядка

$$\begin{vmatrix} a_{1} & c_{1}\\ a_{2} & c_{2} \end{vmatrix}.$$

Чтобы вычислить определитель третьего порядка, нужно каждый элемент строки или столбца, по которым разлагается определитель, умножить на его минор, взятый со знаком плюс или минус в зависимости от того, будет ли сумма номеров зачеркнутых строки и столбца четным или нечетным числом. Например,

$$\Delta=\begin{vmatrix} a_{1} &b_{1} & c_{1}\\ a_{2} &b_{2} & c_{2} \\ a_{3} &b_{3} & c_{3} \end{vmatrix}=a_{1}\begin{vmatrix} b_{2} &c_{2} \\ b_{3} & c_{3} \end{vmatrix}-a_{2}\begin{vmatrix} b_{1} &c_{1} \\ b_{3} & c_{3} \end{vmatrix}+a_{3}\begin{vmatrix} b_{1} & c_{1}\\ b_{2} & c_{2} \end{vmatrix}$$

- разложение определителя Δ по первому столбцу.
Пример. Вычислить определитель

$$\begin{vmatrix} 3 & \; 2 &\; 2\\ 1 &-5 &-8 \\ 4& \; 2 & \; 1 \end{vmatrix}.$$

Решение.

$$\begin{vmatrix} 3 & \; 2 &\; 2\\ 1 &-5 &-8 \\ 4& \; 2 & \; 1 \end{vmatrix}=-\begin{vmatrix} 2 & 2\\ 2 & 1 \end{vmatrix}-5\begin{vmatrix} 3 & 2\\ 4& 1 \end{vmatrix}+8\begin{vmatrix} 3 & 2\\ 4 & 2 \end{vmatrix}=2+25-16=11.$$

Основные свойства определителей третьего порядка.
Свойство 1. Величина определителя не изменится, если за¬писать столбцы вместо строк, а строки вместо столбцов.
Свойство 2. При перестановке двух столбцов или строк определитель меняет знак.
Свойство 3. Чтобы умножить определитель на какое-нибудь число, достаточно умножить на это число все элементы какой-нибудь одной строки или какого-нибудь одного столбца.
Свойство 4. Если в определителе имеются две одинаковых строки или два одинаковых столбца, то он равен нулю.
Свойство 5. Величина определителя не изменится, если к элементам некоторого ряда прибавить элементы параллельного ряда, предварительно умножив их на постоянный множитель.