Задача №1. Написать канонические уравнения кривых второго пооядка:
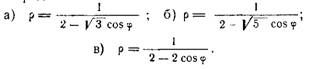
Решение.
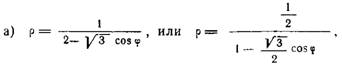
откуда ![]()
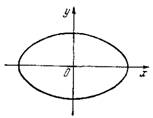
Следовательно, данное уравнение есть уравнение эллипса.
Имеем систему уравнений:
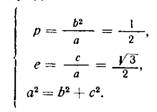
Решив эту систему:
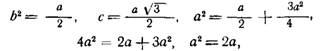
получим: а = 2, b = 1.
Каноническим уравнением эллипса будет:
![]()
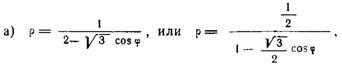
откуда ![]()
Следовательно, данное уравнение есть уравнение гиперболы (рис.2).
Имеем систему уравнений:
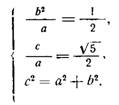
Решив эту систему:
![]()
5а² = 4а²+2а, а²=2а,
получим: а = 2, b² = 1, b = 1.
Каноническим уравнением гиперболы будет:
![]()
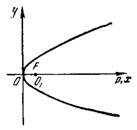
откуда е = 1.
Следовательно, данное уравнение есть уравнение параболы (рис.3).
Имеем р = 1/2.
Каноническим уравнением параболы будет: у²=2рх, y²=х.
Ответ:
![]()
Решение этой задачи подробно изложено в следующем видео
Задача №2. Вычислить длину полуосей и расстояние между фокусами эллипса
![]()
Решение. Преобразуем данное уравнение
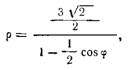
откуда
![]()
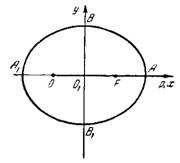
Но
![]()
Имеем следующую систему уравнений:
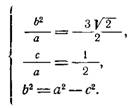
Решив ее, найдем
![]()
Ответ: ![]()
Решение этой задачи подробно изложено в следующем видео







