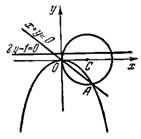
Задача №1. Составить уравнение геометрического места точек, одинаково удаленных от точки F (-2; 0) и от прямой х + 6 = 0. Найти точки пересечения этой кривой с осями координат.
Решение. Обозначим произвольную точку искомой кривой через Р(х;у), ее расстояние до точки F равно:
![]()
а до прямой MN равно: d = x + 6.
Так как PF и d по условию равны, то приравняв их, получим уравнение:
![]()
Упростим его:
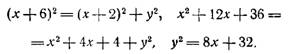
Полученное уравнение есть уравнение параболы, симметричной относительно оси Ох. Вершина ее находится в точке А (—4; 0). (В уравнении параболы положив y = 0, найдем х = -4.)
Точки пересечения параболы с осью Оу найдем, положив в уравнении
![]()
таким образом, имеем ![]()
Ответ:
![]()
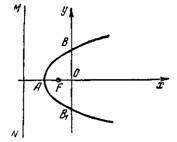
Задача №2. Написать уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой х + у = 0 и окружности х²+у²-4х=0 и симметрична относительно оси Оу.
Решение. Найдем точки пересечения заданных линий, решив совместно уравнения:
![]()
Точки пересечения О (0; 0) и А (2; —2). Так как парабола проходит через точку О (0; 0) и симметрична относительно оси Оу, то в этой точке будет находиться вершина параболы. Поэтому уравнение параболы имеет вид:
Так как парабола проходит через точку А (2; -2), то координаты этой точки удовлетворяют уравнению параболы:
Таким образом, уравнением параболы будет: x²=-2у.
Уравнение директрисы ![]()
Подставив значение р, получим у =1/2 или 2y-1=0
Ответ: х²=-2у; 2y-1=0.
Решения этих задач подробно изложено в следующем видео
Задача №2. Струя воды фонтана достигает наибольшей вы¬соты 4 м на расстоянии 0,5 м от вертикали, проходящей через точку О выхода струи. Найти высоту струи над горизонталью Ох на расстоянии 0,75 м от точки О.
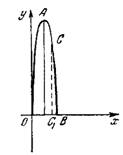
Решение. Струя воды фонтана имеет форму параболы, вершина которой находится в точке А (0,5; 4). Ось симметрии параболы параллельна оси Оу, поэтому уравнение параболы имеет вид:
![]()
Подставив значения х₀ и у₀, получим:
Для определения р мы можем в уравнение подставить вместо текущих координат координаты точки О (0; 0) (так как струя фонтана выходит из точки О)
Таким образом, уравнение параболы имеет вид:
![]()
или после преобразований у = 16(x-x²).
Абсцисса точки С равна 0,75. Ординату высоты струи над точкой С найдем, использовав уравнение параболы:
у = 16(0,75 — 0,75²) = 16·0,75(1 - 0,75)= 12·0,25 = 3.
Ответ: h = 3 м.
Решение этой задачи подробно изложено в следующем видео