Пример 1. Построить на одном чертеже графики функций  и
и  . Путем сложения ординат полученных линий построить график функции
. Путем сложения ординат полученных линий построить график функции  .
.
Решение. График всякой линейной функции есть прямая линия. Поэтому для построения графика первой данной функции, которая является линейной, достаточно иметь две пары соответствующих друг другу значений переменных, т. е. две точки.
Для построения графика второй данной функции берем значения  в радианах, а значения
в радианах, а значения  из тригонометрических таблиц. Учитываем также периодичность этой функции: построив ее график на протяжении одного периода
из тригонометрических таблиц. Учитываем также периодичность этой функции: построив ее график на протяжении одного периода ![\displaystyle [0;2\pi ]](https://math-helper.net/wp-content/plugins/latex/cache/tex_bbec00c088b8955d24c863b5fa7765aa.gif) , затем повторяем его. Алгебраически складывая ординаты точек линий
, затем повторяем его. Алгебраически складывая ординаты точек линий

 и
и  , имеющих одинаковые абсциссы
, имеющих одинаковые абсциссы  , получим искомый график функции
, получим искомый график функции  (рис.1)
(рис.1)
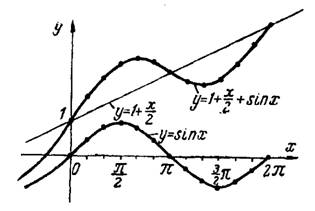
Рис.1
Пример 2. Найти приближенные значения корней функции  , построив ее график на отрезке [—1;3].
, построив ее график на отрезке [—1;3].
Решение. Корни функции, т. е. значения аргумента, обращающие ее в нуль, можно найти как абсциссы точек пересечения графика функции с осью абсцисс, так как в этих точках  .
.
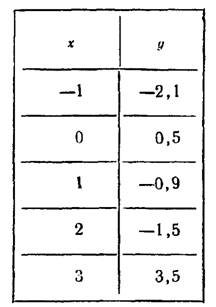
Составив таблицу числовых значений переменных  и
и  , построим график данной функции (рис.2).
, построим график данной функции (рис.2).
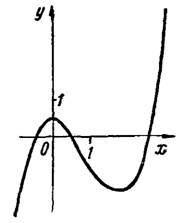
Из чертежа находим искомые приближенные значения корней функции: 







